Chapter 3 Algorithm for the Closest and Shortest Vector Problems
3.1 Babai’s Rounding Technique
Theorem 3.1.1. Given a vector we can write $\underline{\omega}=\sum_{i=1}^{n}\alpha_{i}\underline{b_{i}}$ with $\alpha_{i}\in R$. The rounding technique is simply to set
$\left|\underline{v}-\underline{w}\right|$ is within an exponential factor of the minimal value if the basis is LLL-Reduced. The method trivially generalises to non-full-rank lattices as long as $\underline{\omega}$ lies in the R-span of the basis.
Theorem 3.1.2. Let $\{\underline{b}_{1},…,\underline{b}_{n}\}$ be an LLL-Reduced basis (with factor $\delta=\frac{3}{4}$) for a Lattice $L\subset R^{n}$. Then the output $\underline{v}$ of the Babai rounding method on input $\underline{\omega}\in R^{n}$ satisfies
for all $\underline{u}\in L$.
3.2 The Embedding Technique
Theorem 3.2.1. Embedding’s solution to the CVP corresponds to integers $l_{1},…,l_{n}$ such that
The idea is to define a lattice L’ that contains the short vector $\underline{e}(\underline{e}=\underline{\omega}-\sum_{i=1}^{n}l_{i}\underline{b_{i}})$. Let $M\in R_{>0}$ (usually let M=1). The lattice L’ is defined by the vectors (which are a basis for $R^{n+1}$)
Hence, we might be able to find $\underline{e}$ by solving the SVP problem in the lattice L’. Then we can solve the CVP by subtracting $\underline{e}$ from $\underline{\omega}$.
Example: the CVP whose basis is for $R^{1}$

add $(\underline{\omega},M)$ to define L’ in $R^{2}$
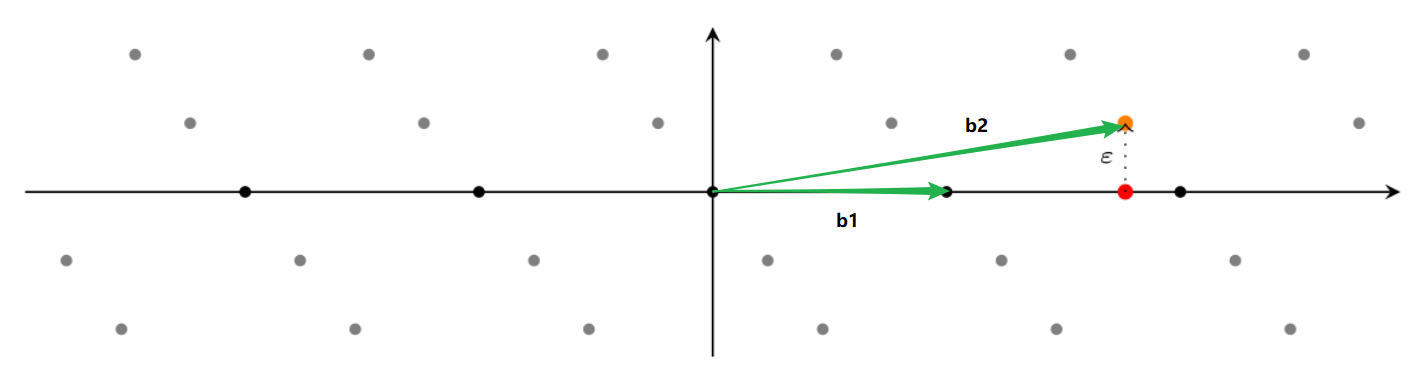
solving the SVP to find $\delta$
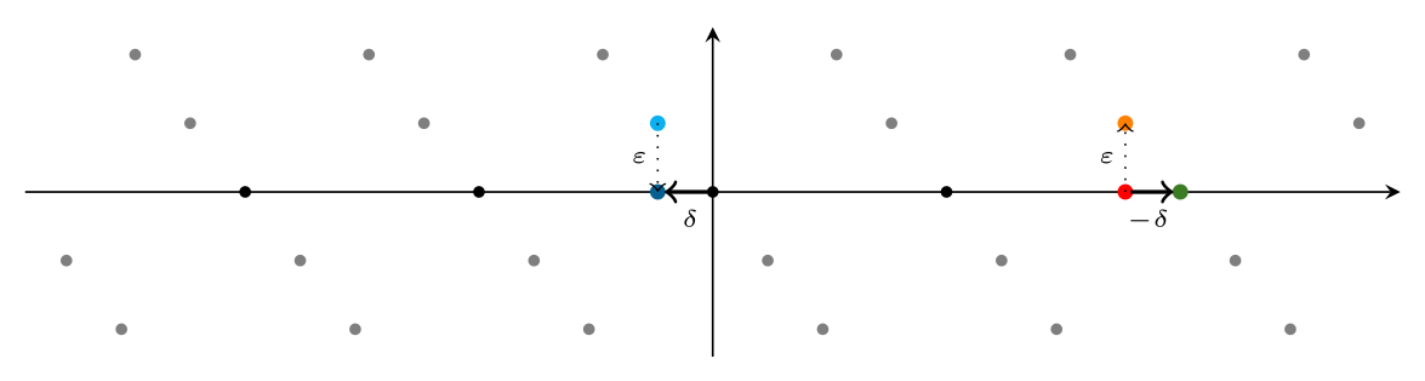
Lemma 3.2.2. Let $\{\underline{b}_{1},…,\underline{b}_{n}\}$ be a basis for a lattice $L\subset Z^{n}$ and donate by $\lambda_1$ the shortest Euclidean length of a non-zero element of L. Let $\underline{\omega}\in R^{n}$ and let $\underline{v}\in L$ be a closest lattice point to $\underline{\omega}$. Define $\underline{e}=\underline{\omega}-\underline{v}$. Suppose that $\left|\underline{e}\right|<\lambda_1/2$ and let $M=\left|\underline{e}\right|$. Then $(\underline{e},M)$ is a shortest non-zero vector in the lattice L’ of the embedding technique.
Proof: All vectors in L’ are of the form
for some $l_{i}\in Z$. It is clear that every non-zero vector with $l_{n+1}=0$ is of length at least $\lambda_{1}$.
Since $\left|(\underline{e},M)\right|^{2}=\left|\underline{e}\right|^{2}+M^{2}=2M^{2}<\frac{\lambda^{2}}{2}$, the vector $(\underline{e},M)$ has length at most $\frac{\lambda_1}{\sqrt{2}}$. Since $\underline{v}$ is a closest vector to $\underline{\omega}$ in the lattice L, $\forall_{\underline{x}\in L},s.t.\left|\underline{e}\right|\leq \left|\underline{e}+\underline{x}\right|$. SVP’s correctness proved.
3.3 Korkine-Zolotarev Bases
Schnorr has developed the block Korkine-Zolotarev lattice basis reduction algorithm, which computes a Korkine-Zolotarev basis for small dimensional projections of the original lattice and combines this with the LLL algorithm. The output basis can be proved to be of a better quality than an LLL-reduced basis. This is the most powerful algorithm for fifinding short vectors in lattices of large dimension.
Chapter 4 Coppersmith’s Method and Related Applications
4.1 Coppersmith’s Method for Modular Univariate Polynomials
4.1.1 First Steps to Coppersmith’s Method
Let $F(x)=x^{d}+a_{d-1}x^{d-1}+…+a_{1}x+a_{0}$ be a monic polynomial of degree d with integer coefficients. Suppose we know that there exist one or more integers $x_{0}$ such that $F(x)\equiv 0(mod\ M)$ and that $x_{0}<M^{\frac{1}{d}}$. The problem is to find all such roots.
Since $|x_{0}^{i}|<M$ for all $0\leq i\leq d$ then, if the coefficients of F(x) are small enough, one might have $F(x_{0})=0$ over Z. In this case, the problem can be easily solved by Newton’s method (round the approximations of the roots to the nearest integer and check whether they are solutions of F(x)). However, we wanna deal with polynomials F(x) having a small solution but whose coefficients are not small.
Coppersmith’s idea is to build from F(x) a polynomial G(x) that still has the same solution $x_{0}$, but which has coefficients small enough.
Theorem 4.1.1. (Howgrave-Graham [296]) Let $M, X\in N$ and let $F(x)=\sum_{i=0}^{d}a_{i}x^{i}\in Z[x]$. Suppose $x_{0}\in Z$ is a solution to $F(x)\equiv 0(mod\ M)$ such that $|x_{0}|<X$. We associate with the polynomial F(x) the row vector $b_F=(a_0,a_{1}X,a_{2}X^{2},…,a_{d}X^{d})$. If $\left|b_{F}\right|<\frac{M}{\sqrt{d+1}}$ then $F(x_{0})=0$.
Proof: Cauchy-Schwarz inequality $\rightarrow\sum_{i=1}^{n}x_{i}\leq \sqrt{n\sum_{i=1}^{n}x_{i}^{2}}$.
So, $|F(x_{0})|=|\sum_{i=0}^{d}a_{i}x_{0}^{i}|\leq \sum_{i=0}^{d}|a_{i}||x_{0}|^{i}\leq \sum_{i=0}^{d}|a_{i}|X^{i}\leq \sqrt{d+1}\left|b_{F}\right|<\sqrt{d+1}\frac{M}{\sqrt{d+1}}=M$.
$\therefore F(x_{0})=0$.
Then how to transform F(x) to G(x) we need?
To do this, consider the d+1 polynomials $G_{i}(x)=Mx^{i}$ for $0\leq i<d$ and F(x). They all have the solution $x=x_{0}$ module M. Define the lattice L with the basis B
Theorem 4.1.2. Let G(x) be the polynomial corresponding to the first vector $\underline{b}_{1}$ in the LLL-Reduced basis for L. Set $c_{1}(d)=2^{-\frac{1}{2}}(d+1)^{-\frac{1}{d}}$. If $X Compared to previous section, some benefits can be obtained by using x-shifts. (Get larger X) Theorem 4.1.3. (Coppersmith) Let $0<\epsilon<min\{0.18,\frac{1}{d}\}$. Let F(x) be a monic polynomial of degree d with one or more small roots $x_{0}$ module M such that $|x_{0}|<\frac{1}{2}M^{\frac{1}{d}-\epsilon}$. Then $x_{0}$ can be found in time bounded by a polynomial in d, $\frac{1}{\epsilon}$ and log(M). Theorem 4.2.1. Let $F(x,y)\in Z[x,y]$ be a polynomial of total degree d (i.e., every monomial $x^{i}y^{j}$ satisfies $i+j\leq d$). Let $X,Y,M\in N$ be such that $XY Theorem 4.3.1. Let $F(x,y)\in Z[x,y]$ and let $d\in N$ be such that $deg_{x}(F(x,y)),deg_{y}(F(x,y))\leq d$. Write For $X,Y\in N$, we define If $XY<W^{\frac{2}{3d}}$ then there is an algorithm that takes as input F(x,y),X,Y, runs in time (bit operations) bounded by a polynomial in log(W) and $2^{d}$, and outputs all pairs $(x_{0},y_{0})\in Z^{2}$ such that $F(x_{0},y_{0})=0,|x_0|\leq X,|y_0|\leq Y$. It is necessary to use padding schemes for RSA encryption and one simple proposal for k-bit RSA moduli is to take a k’ bit message and pad it by putting (k-k’-1) ones to the left hand side of it. This padding scheme is sometimes called fixed pattern padding. Then if $|x|<\frac{1}{2}N^{\frac{1}{e}}(k’<\frac{k}{e}-1)$, Coppersmith’s method can solve it in polynomial time. Given an approximation $\tilde{p}$ to p such that $p=\tilde{p}+x_{0}$ where $|x_{0}|<X$. The polynomial $F(x)=(x+\tilde{p})$ has a small solution module p. The problem is that we don’t know p, but we do know a multiple of p (i.e., N). The idea is to form a lattice corresponding to polynomials that have a small root modulo p and to apply Coppersmith’s method to find this root $x_0$. Theorem 4.4.1. Let N=pq with p<q<2p. Let $0<\epsilon <\frac{1}{4}$, and suppose $\tilde{p}\in N$ is such that $|p-\tilde{p}|\leq \frac{1}{2\sqrt{2}}N^{\frac{1}{4}-\epsilon}$. Then given N and $\tilde{p}$ one can factor N in time polynomial in log(N) and $\frac{1}{\epsilon}$. By constructing lattice whose basis including $NX^{i},X^{i}F(X)$. Example 4.4.2. (Takagi-RSA) Let $N=p^{r}q$ where p and q are primes and r>1. Suppose the public exponent e in RSA is small. One can compute $c^{d}(mod\ N)$ as follows. Let $d_{p}\equiv d(mod\ p-1)$ and $d_{q}\equiv d(mod\ q-1)$. One first computes $m_{p}=c^{d_{p}}(mod\ p)$ and $m_{q}=c^{d_{q}}(mod\ q)$. Then we can determine $m(mod\ p^{r})$ from $m_p$ by using Hensel lifting. If we have determined $m_{i}\equiv m (mod\ p^{i})$ then we lift to a solution modulo $p^{i+1}$ by writing $m_{i+1}=m_{i}+kp^{i}$, where k is a variable. Then gives $k\ mod(p^{i+1})$. The equation above is only efficient when e is small. If e is large then the Hensel lifting stage is no faster than just computing $c^{d(mod\ \varphi(p^{r}))}(mod\ p^{r})$ directly. Coppersmith’s method can be used to factor integers of the form $N=p^{r}q$ when r is large. If one knows r and an approximation $\tilde{p}$ to p then there is a small root of the polynomial equation It is shown that if $r\geq log(p)$ then the algorithm runs in polynomial-time.4.1.2 The Full Coppersmith Method
4.2 Multivariate Modular Polynomial Equations
4.3 Bivariate Integer Polynomials
4.4 Some Applications of Coppersmith’s method
4.4.1 Fixed Padding Schemes in RSA
4.4.2 Factoring N = pq with Partial Knowledge of p
4.4.3 Factoring $p^{r}q$
