Stream Cipher - Many Time Pad

Theorem

  • 流密钥循环使用

  • 猜测密钥长度

    Hamming Distance（二进制下两个等长字符串的比特位差异）

    大小写英文字符两两的平均Hamming距离为2 ~ 3，而任意字符两两的平均Hamming距离为4

    取合适的密钥长度上下界，进行分组计算汉明距离

    将二元组(key_length, distance)按distance升序排列，取前五组验证即可

  • 逐字节破解密钥

    在猜测的密钥长度基础上，分割Cipher（用同一密钥字节加密的密文归入同组）

    字频分析

    遍历range(0xff)，和标准频率表（含空格和字母）内积最大的即猜测为正确密钥字节

    因为不正确密钥字节下也可能内积很大，所以进行如下filter：

    • decode(‘ascii’)出错 => return 0

    • cipher分组里为空格或字母的字符总数 < len(cipher_fragment) // 1.5 => return 0

    爆破空格

    基于空格和小写字母异或结果为对应大写字母，和大写字母异或结果为对应小写字母这一特性

    对同一分组的cipher进行两两异或（相当于plain两两异或），记录每个字符与其他所有字符异或结果落在落在大小写字母和0x00上的次数，即可认为最大次数对应的字符位置上的明文为空格

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
import string
from binascii import hexlify, unhexlify

std_rate = {' ': 0.18399868388580254, 'a': 0.06528332604415538, 'b': 0.012531342868095015, 'c': 0.021018439349774747, 'd': 0.03523431934577844, 'e': 0.10261742470196494, 'f': 0.019179805952664334, 'g': 0.016178672025026573, 'h': 0.050890812568726566, 'i': 0.056467348737766584, 'j': 0.0011847320400802188, 'k': 0.006037640287976256, 'l': 0.03310705983030898,
            'm': 0.02089774777877722, 'n': 0.056334978507447564, 'o': 0.06194486601507346, 'p': 0.014653281404481763, 'q': 0.0009593791262805568, 'r': 0.048625794552908115, 's': 0.051741663225580235, 't': 0.07413556318261176, 'u': 0.023188985607049396, 'v': 0.008010827191217628, 'w': 0.018155155658972653, 'x': 0.0014651754741116037, 'y': 0.015511271998835988, 'z': 0.0006457026385315064}


def bytes_xor(x, y):
    if len(y) > len(x):
        x, y = y, x
    return bytes([i ^ j for i, j in zip(x[:len(y)], y)])


def hamming_distance(x, y):
    dis = 0
    for byte in bytes_xor(x, y):
        dis += bin(byte).count('1')
    return dis


def get_key_length(cipher):
    average_distances = []
    for key_length in range(2, 40):
        cipher_fragments = []
        for i in range(10):
            if key_length * (i + 1) > len(cipher):
                break
            cipher_fragments.append(
                cipher[key_length * i: key_length * (i + 1)])
        distance = 0
        for i in range(len(cipher_fragments) - 1):
            distance += hamming_distance(
                cipher_fragments[i], cipher_fragments[i + 1])
        distance /= (key_length * len(cipher_fragments))
        average_distances.append((key_length, distance))
    average_distances.sort(key=lambda x: x[1])
    return average_distances


'''
# 字频分析
def dot_multiply(p):
    rate = [0] * 27
    tmp_len = 0
    for _ in p:
        try:
            _ = bytes([_]).decode('ascii')
        except:
            return 0
        _ = _.lower()
        if _ in std_rate:
            tmp_len += 1
            if _ == ' ':
                rate[0] += 1
            else:
                rate[ord(_) - ord('a') + 1] += 1
    if not tmp_len or tmp_len < len(p) // 1.5:
        return 0
    rate = [i / tmp_len for i in rate]
    res = rate[0] * std_rate[' ']
    for i in range(1, 27):
        res += rate[i] * std_rate[chr(ord('a') + i - 1)]
    return res


def crack_key_fragment(cipher_fragment):
    max_dotmul_res = 0
    pro_key_fragment = 0
    for key_fragment in range(0xff):
        key_set = [key_fragment] * len(cipher_fragment)
        plain_fragment = bytes_xor(key_set, cipher_fragment)
        dotmul_res = dot_multiply(plain_fragment)
        if dotmul_res > max_dotmul_res:
            max_dotmul_res = dotmul_res
            pro_key_fragment = key_fragment
    return pro_key_fragment


def crack_key(cipher, average_distances):
    for key_length, _ in average_distances[:5]:
        key = []
        cipher_fragments = [[] for _ in range(key_length)]
        for i, byte in enumerate(cipher):
            cipher_fragments[i % key_length].append(byte)
        for cipher_fragment in cipher_fragments:
            key.append(crack_key_fragment(cipher_fragment))
        print(bytes(key))
'''


# 爆破空格
def crack_key_fragment(cipher_fragment):
    max_possible = 0
    pro_space = 0  # 空格下标索引
    letters = string.ascii_letters.encode('ascii')
    for i in range(len(cipher_fragment)):
        possible = 0
        for j in range(len(cipher_fragment)):
            if i == j:
                continue
            _ = cipher_fragment[i] ^ cipher_fragment[j]
            if _ in letters or _ == 0:
                possible += 1
        if possible > max_possible:
            max_possible = possible
            pro_space = i
    return cipher_fragment[pro_space] ^ 0x20


def crack_key(cipher, average_distances):
    for key_length, _ in average_distances[:5]:
        key = []
        cipher_fragments = [[] for _ in range(key_length)]
        for i, byte in enumerate(cipher):
            cipher_fragments[i % key_length].append(byte)
        for cipher_fragment in cipher_fragments:
            key.append(crack_key_fragment(cipher_fragment))
        print(bytes(key))


def main():
    masked_cipher = b'input your masked_cipher here'
    salt = b'input your salt here'
    cipher = bytes_xor(masked_cipher, salt *
                       (len(masked_cipher) // len(salt) + 1))
    average_distances = get_key_length(cipher)
    crack_key(cipher, average_distances)


if __name__ == "__main__":
    main()

LFSR - Basis

Theorem

单个lfsr且已知抽头序列的情况下，只要有任意n个比特的流信息，即可轻易恢复完整流

等价于解n元1次方程（18年国赛streamgame）

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# In[26]
mask = 0b10100100000010000000100010010100
mask_bin = bin(mask)[2:].rjust(32, '0')
feedback = []
for i in range(32):
    if mask_bin[i] == '1':
        feedback.append(i)
feedback.append(32)
delta = feedback[0] + 1
feedback = [_ - delta for _ in feedback]

# In[27]
cipher = open("key", "rb").read()

# In[28]
cipher_bin = ''
for c in cipher:
    cipher_bin += bin(c)[2:].rjust(8, '0')
    
# In[30]
cur = cipher_bin[:feedback[-1] + 1]
flag = ''
for i in range(32):
    right = [cur[j] for j in feedback[1:]]
    left = str(right.count('1') % 2)
    flag = left + flag
    cur = left + cur[:-1]
flag

# Out[36]
'00110000011111010101001001100100'

LFSR - Correlation Attack

Theorem

实际使用的lfsr往往是多个lfsr并行，并通过代数运算F来获得密钥流

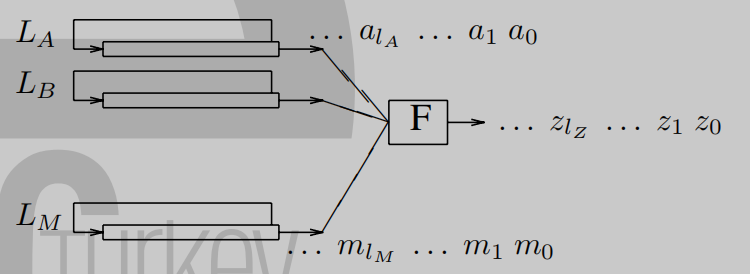
列出代数运算F的真值表，即可得到相关系数$p_{1},…,p_{n}$

一般认为在$p_{i}\geq 0.6$时，能使用相关攻击对第i个lfsr的密钥流实现恢复($p_{i}=0.75$时效果较好)

相关攻击使得复杂度从$\prod$优化为$\sum$，余下相关系数趋于0.5的lfsr采用暴力枚举即可

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
import threading
import time

cipher = ''
R1_mask, R2_mask, R3_mask = 0x10020, 0x4100c, 0x100002
R1_partMask, R2_partMask, R3_partMask = 0xffffff, 0xffffff, 0xffffff
n1, n2, n3 = 17, 19, 21
R = [0, 0, 0]
crack_state = [False, False, False]  # 相关攻击是否已完成(退出其他线程)
start = time.clock()


def init_stream(read_length):
    global cipher
    cipher_bytes = open('cipher', 'rb').read(read_length)
    cipher = ''.join(bin(c)[2:].rjust(8, '0') for c in cipher_bytes)


def lfsr(R, mask, partMask):
    output = (R << 1) & partMask
    i = (R & mask) & partMask
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)
        i = i >> 1
    output ^= lastbit
    return (output, lastbit)


def single_lfsr(R, mask, partMask, N):
    ret = ''
    for i in range(N):
        (R, out) = lfsr(R, mask, partMask)
        ret += str(out)
    return ret


def single_round(R1, R2, R3):
    (R1_new, x1) = lfsr(R1, R1_mask, R1_partMask)
    (R2_new, x2) = lfsr(R2, R2_mask, R2_partMask)
    (R3_new, x3) = lfsr(R3, R3_mask, R3_partMask)
    return (R1_new, R2_new, R3_new, (x1 * x2) ^ ((x2 ^ 1) * x3))


def encrypt(R1, R2, R3, N):
    ret = ''
    for i in range(N):
        (R1, R2, R3, out) = single_round(R1, R2, R3)
        ret += str(out)
    return ret


def correlation(single_cipher, cipher):
    assert(len(single_cipher) == len(cipher))
    count = 0
    for i, j in zip(single_cipher, cipher):
        if i == j:
            count += 1
    return count / len(cipher)


def crack_p():
    p1, p2, p3 = 0, 0, 0
    for x1 in range(2):
        for x2 in range(2):
            for x3 in range(2):
                value = (x1 * x2) ^ ((x2 ^ 1) * x3)
                p1 += x1 ^ value ^ 1
                p2 += x2 ^ value ^ 1
                p3 += x3 ^ value ^ 1
    return (p1 / 8, p2 / 8, p3 / 8)


def crack_key(p, mask, partMask, low, high, index):
    global R
    global crack_state
    for guess_R in range(low, high):
        if crack_state[index - 1] == True:
            return
        single_cipher = single_lfsr(guess_R, mask, partMask, len(cipher))
        correlation_value = correlation(single_cipher, cipher)
        if correlation_value >= (p - 0.05) and correlation_value <= (p + 0.05):
            print((hex(guess_R)[2:].rjust(6, '0'), correlation_value))
            R[index - 1] = guess_R
            crack_state[index - 1] = True
            end = time.clock()
            print('cost {}s'.format(end - start))
            return


def brute_force(low, high):
    global R
    global crack_state
    for guess_R in range(low, high):
        if crack_state[1] == True:
            return
        guess_cipher = encrypt(R[0], guess_R, R[2], len(cipher))
        if guess_cipher == cipher:
            R[1] = guess_R
            crack_state[1] = True
            return


def main():
    init_stream(256)
    # crack_p (step 1)
    (p1, p2, p3) = crack_p()
    print((p1, p2, p3))
    # correlation attack (step 2)
    threads = []
    low = 2**(n1 - 1)
    crack_length = low // 16
    high = low + crack_length
    for i in range(16):
        t = threading.Thread(target=crack_key, args=(
            p1, R1_mask, R1_partMask, low, high, 1))
        threads.append(t)
        low = high
        high += crack_length
    low = 2**(n3 - 1)
    crack_length = low // 16
    high = low + crack_length
    for i in range(16):
        t = threading.Thread(target=crack_key, args=(
            p3, R3_mask, R3_partMask, low, high, 3))
        threads.append(t)
        low = high
        high += crack_length
    for t in threads:
        t.start()
    for t in threads:
        t.join()
    # brute_force (step 3)
    threads = []
    low = 2**(n2 - 1)
    crack_length = low // 16
    high = low + crack_length
    for i in range(16):
        t = threading.Thread(target=brute_force, args=(low, high))
        threads.append(t)
        low = high
        high += crack_length
    for t in threads:
        t.start()
    for t in threads:
        t.join()
    end = time.clock()
    print('cost {}s'.format(end - start))
    print(hex(R[0])[2:].rjust(6, '0'), end='')
    print(hex(R[1])[2:].rjust(6, '0'), end='')
    print(hex(R[2])[2:].rjust(6, '0'), end='')


if __name__ == '__main__':
    main()
1
2
3
4
5
6
7
(0.75, 0.5, 0.75)
('01b9cb', 0.74755859375)
cost 30.8923027s
('16b2f3', 0.74169921875)
cost 362.5205596s
cost 436.23293620000004s
01b9cb05979c16b2f3

More

exp对应的是强网杯streamgame3，在pypy3下大约七八分钟能出答案，但python3估计就有点儿慢了-.-

网上现在传的版本大多也都只是相关攻击，顶多在多线程上进行部分优化

快速相关攻击的A算法原理理解很容易，但我编写脚本测试后发现出不来…暂时搁置

安全客上有一篇讲LFSR相关攻击的文章，分别用了开普敦大学的轮子和z3约束来进行求解，链接如下

https://www.anquanke.com/post/id/184828

LFSR - Known Plain Attack

Theorem

LFSR的KPA问题（已知明文长度要大等于两倍的LFSR级数n）

  • 对LFSR级数n进行range(2, len(stream) // 2)上的爆破（stream是已知明文段）
  • 因为$len(stream)//2\geq n$，所以每个猜测级数i下均对应至少i个i元线性方程（系数矩阵秩<i情况一般不考虑）
  • LFSR的下一位只受当前n位和抽头序列影响，因此得到n个GF(2)上形如$\sum_{i=1}^{n}p_{i}$, if stream[i]==1的线性方程，于是抽头序列$\\{p_{i}\\}$获知，恢复全部明文并校验即可

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
from z3 import *

p0, p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11, p12, p13, p14, p15, p16, p17, p18, p19, p20, p21, p22, p23, p24, p25, p26, p27, p28, p29, p30, p31, p32, p33, p34, p35, p36, p37, p38, p39, p40, p41, p42, p43, p44, p45, p46, p47 = BitVecs(
    'p0 p1 p2 p3 p4 p5 p6 p7 p8 p9 p10 p11 p12 p13 p14 p15 p16 p17 p18 p19 p20 p21 p22 p23 p24 p25 p26 p27 p28 p29 p30 p31 p32 p33 p34 p35 p36 p37 p38 p39 p40 p41 p42 p43 p44 p45 p46 p47', 1)
p = [p0, p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11, p12, p13, p14, p15, p16, p17, p18, p19, p20, p21, p22, p23, p24,
     p25, p26, p27, p28, p29, p30, p31, p32, p33, p34, p35, p36, p37, p38, p39, p40, p41, p42, p43, p44, p45, p46, p47]


def init_stream(known_plain, known_cipher):
    assert(len(known_plain) == len(known_cipher) and len(known_plain) <= 24)
    known_plain_dec = int(known_plain, 16)
    #known_plain_dec = int('89504E470D0A1A0A0000000D', 16)
    known_cipher_dec = int(known_cipher, 16)
    return bin(known_plain_dec ^ known_cipher_dec)[2:].rjust(4 * len(known_plain), '0')


def crack_key(stream, key_length):
    assert(len(stream) >= 2 * key_length)
    solver = Solver()
    #var_name = ['p' + str(i) for i in range(key_length)]
    #exec('{}=BitVecs(\'{}\',1)'.format(",".join(var_name), " ".join(var_name)))
    for i in range(len(stream) - key_length):
        cur = stream[i: i + key_length + 1]
        equation = ''
        for j in range(key_length):
            if cur[j] == '1':
                equation += 'p' + str(j) + '+'
            else:
                pass
        if len(equation):
            equation = equation[:-1] + ' == ' + str(cur[-1])
            solver.add(eval(equation))
    if solver.check() == sat:
        m = solver.model()
        feedback = ''.join([str(m[p[i]]) for i in range(key_length)])
        #print('[{}]: ini_key = \'{}\' ; feedback = \'{}\''.format(str(key_length), stream[:key_length], feedback))
        return (stream[:key_length], feedback)
    else:
        return (False, False)


def lfsr(cur, feedback):
    cur_num = int(cur, 2)
    output = (cur_num << 1) & ((1 << len(feedback)) - 1)
    i = (cur_num & int(feedback, 2)) & ((1 << len(feedback)) - 1)
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)
        i = i >> 1
    output ^= lastbit
    output = bin(output)[2:].rjust(len(cur), '0')
    return (output, lastbit)


def get_byte(cur, feedback):
    if len(cur) >= 8:
        byte = int(cur[:8], 2)
        for i in range(8):
            cur, lastbit = lfsr(cur, feedback)
        return (cur, byte)
    else:
        byte = cur
        for i in range(8 - len(cur)):
            cur, lastbit = lfsr(cur, feedback)
            byte += str(lastbit)
        return (cur, int(byte, 2))


def main():
    cipher = open('lfsr.png.encrypt', "rb").read()
    # kpa_attack for length(hex) <= 24
    stream = init_stream('89504E470D0A1A0A0000000D',
                         'e63b037e74c01aeefd6552ef')
    for key_length in range(2, len(stream) // 2):
        key, feedback = crack_key(stream, key_length)
        if (key, feedback) != (False, False):
            cur = key
            fw = open('lsfr_{}.png'.format(key_length), 'wb')
            plain = b''
            for i in range(len(cipher)):
                cur, byte = get_byte(cur, feedback)
                plain += bytes([cipher[i] ^ byte])
            fw.write(plain)
            fw.close()
            print('lsfr_{}.png ok!'.format(key_length))


if __name__ == "__main__":
    main()

More

exp对应2020i春秋公益赛的一道lfsr-kpa（已知png文件头，与cipher异或即可将问题转化为lfsr-kpa问题）

lfsr-kpa可以不局限于开头，密钥流中任意段已知2n个bit均可进行抽头序列的猜测（lfsr在已知n个连续比特和抽头序列的情况下一定能恢复完整密钥流）