Summary-of-Crypto-in-CTF(Block)

Feistel-SP结构

下图即为Feistel-SP结构的通用模型，其中F函数是SP结构

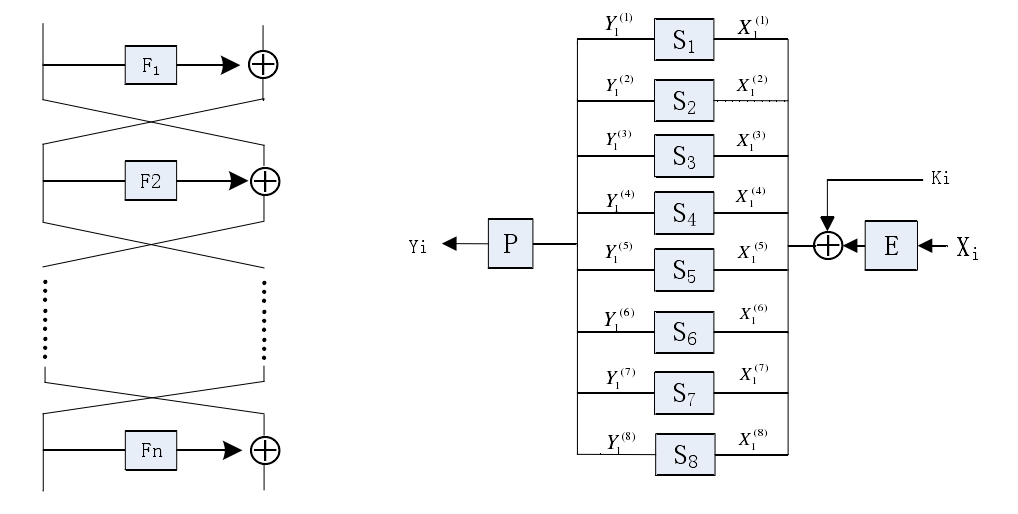
注：$X_{i}^{1}$和$Y_{i}^{1}$分别表示通过$S_{1}$的输入和输出向量，$X_{i}^{j},Y_{i}^{j}$类似.

线性分析

Theorem

基本方法即为寻找一个给定密码系统下，具有如下形式的有效线性表达式

$P[i_{1},...,i_{a}]\oplus C[j_{1},...,j_{b}]=K[k_{1},...,k_{c}]$

($i_{1},…,i_{a};j_{1},…,j_{b};k_{1},…,k_{c}$均为固定比特位)

设$X_{1},X_{2},…,X_{k}$为$\{0,1\}$上的独立随机变量，$Pr(X_{i}=0)=p_{i},Pr(X_{i}=1)=1-p_{i}$，则用分布偏差来表示其概率分布，定义如下

$\epsilon_{i}=p_{i}-\frac{1}{2}$

[堆积引理] - $Pr(X_{1}\oplus …\oplus X_{n}=0)=\frac{1}{2}+2^{n-1}\prod_{i=1}^{n}\epsilon_{i}$，或表示为$\epsilon_{1,2,…,n}=2^{n-1}\prod_{i=1}^{n}\epsilon_{i}$.

利用堆积引理，我们即可以对每轮变换中偏差最大的线性逼近式进行组合，组合后的线性逼近式也将拥有最佳的偏差，即为要找的最佳线性逼近式

[SPN]

下为单轮SPN的示意图

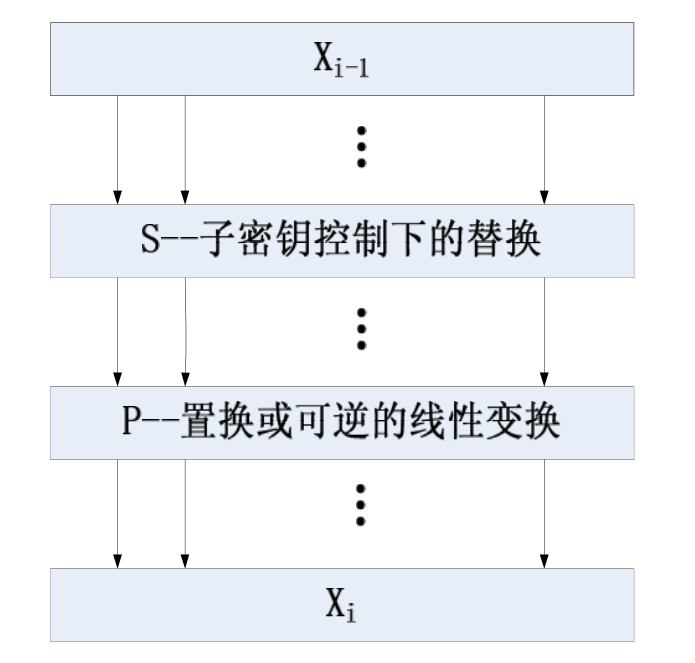
可见非线性结构只有S盒，因此只对其作偏差估计，具体方法如下（假设S盒为16*16）：

将输入的线性近似表示为$a_{1}\cdot X_{1}\oplus a_{2}\cdot X_{2}\oplus …\oplus a_{8}\cdot X_{8}(a_{i}\in \{0,1\})$，对应的，我们也将输出线性近似表示为$b_{1}\cdot Y_{1}\oplus b_{2}\cdot Y_{2}\oplus …\oplus b_{8}\cdot Y_{8}(b_{i}\in \{0,1\})$，穷举所有组合$(a,b)$对应的使得线性近似输入$\oplus$线性近似输出=0的偏差 (256*256)

偏差计算公式$\epsilon(a,b)=(N_{L}(a,b)-128)/256$（$N_{L}(a,b)$为固定(a,b)下，满足上述条件的(X,Y)的个数）

我们的目的就是要找到$|\epsilon(a,b)|_{max}$对应的线性表达式，将其作为该单个S盒下的最佳线性估计

以下面的SPN网络进行讨论分析：

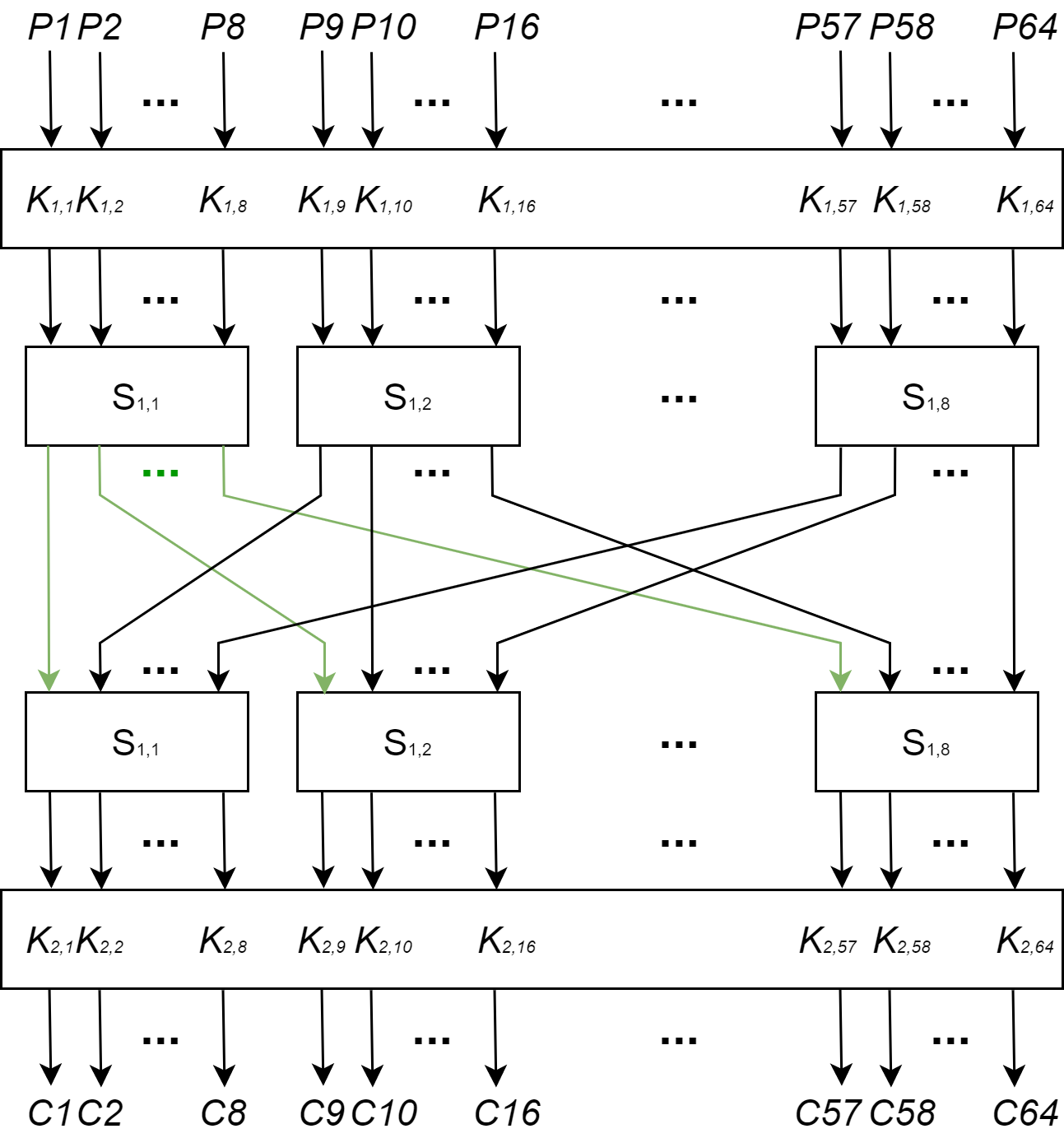
中间的P盒如下：

$\left[ \begin{matrix} 1 & 9 & 17 & 25 & 33 & 41 & 49 & 57\\ 2 & 10 & 18 & 26 & 34 & 42 & 50 & 58\\ ... & ... & ... & ... & ... & ... & ... & ...\\ 8 & 16 & 24 & 32 & 40 & 48 & 56 & 64 \end{matrix} \right]$

为方便分析，我们假设$S_{11}=S_{12}=…=S_{18}$，在找合适的线性逼近前，我们要知道以下两点：

每个线性逼近对应的密钥子集猜测空间不能过大（这里我们使得每个线性逼近表达式里的$C_{i}$满足$8j< i\leq 8(j+1)$，j在每次猜测下各自固定）
涉及线性估计的S盒不能过多（堆积引理$\epsilon_{1,2,…,n}=2^{n-1}\prod_{i=1}^{n}\epsilon_{i}$可知，总偏移量的绝对值会随着n的增大而减小，总偏移量过小会使得在猜测密钥时的成功率极低）

因此我们选择分别对应$S_{11}$八个输出的八个$S_{11}$的最大偏差线性估计，来进行八个第二轮子密钥的猜测（基于不正确的随机密钥会使得测试的明密文对中，满足线性表达式的概率趋于$\frac{1}{2}$，即偏差减小），总的猜测空间为256*8

以$K_{2,1},K_{2,2},…,K_{2,8}$为例，取$u_{1}$为$S_{21}^{-1}(C_{1}\oplus K_{2,1}||C_{2}\oplus K_{2,2}||…||C_{8}\oplus K_{2,8})$的最高位比特

从上述S盒的分析得出$S_{11}$固定$b=10000000$时，最大偏差线性估计对应的$a(a_{1}a_{2}a_{3}a_{4}a_{5}a_{6}a_{7}a_{8})$，因为$K_{1,i}s$异或为定值(0/1)，故不予加入线性表达式，$u_{2}$取为$P_{a_{i}}s$的异或$(a_{i}均等于1)$

密钥空间为256，且每次取相同10000组数据进行线性分析，则假设使得$u_{1}\oplus u_{2}=0$成立的组数为N，$bias=|\frac{N-5000}{10000}|$，很大概率下，$bias_{max}$对应的即为正确密钥

第二轮子密钥完全恢复后，任取一组明密文对即可轻易恢复第一轮子密钥，线性分析结束

exp

以NPUCTF2020出的EzSPN为例

import os, sys
from binascii import hexlify, unhexlify
from pwn import *


SZ = 8
offset = [[0 for i in range(256)] for i in range(256)]  #Sbox线性估计offset
linearInput = []
sbox, sboxi, plain, cipher = [], [], [], []
enc_flag = None
coef = [15, 11, 155, 119, 11, 99, 83, 249]


def getData(ip, port):
    global enc_flag, sbox, sboxi
    io = remote(ip, port)
    sbox_str = io.recvline()
    sbox = eval(sbox_str)
    for i in range(256):
    	sboxi.append(sbox.index(i))
    enc_flag = io.recvline().strip().decode("utf8")
    for i in range(10000):
        print("[+] Getting data...({}/10000)".format(i))
        pt = hexlify(os.urandom(8)).decode("utf8")
        plain.append(pt)
        io.sendline(pt)
        ct = io.recvline().strip().decode("utf8")
        cipher.append(ct)
    io.close()


def doxor(l1, l2):
    return [x[0] ^ x[1] for x in zip(l1, l2)]

# 线性层
def trans(blk):
    res = []
    for k in range(0, SZ, 8):
        cur = blk[k:k+8]
        cur = [(cur[i] * coef[i]) % 256 for i in range(8)]
        bits = [bin(x)[2:].rjust(8, '0') for x in cur]
        bits = bits[-1:] + bits[:-1]
        for i in range(8):
            res.append(int(''.join([x[i] for x in bits]), 2))
    return res


def bitxor(n, mask):
    bitlist = [int(x) for x in bin(n & mask)[2:]]
    return bitlist.count(1) % 2

# Sbox线性估计
def linearSbox():
    global linearInput	
    for i in range(256):
        si = sbox[i]
        for j in range(256):
            for k in range(256):
                a = bitxor(i, j) # 线性估计输入
                b = bitxor(si, k) # 线性估计输出 
                if a == b:
                    offset[j][k] += 1
    for i in range(256):
        offset[i] = [abs(x - 128) / 256 for x in offset[i]]
    for linearOutput in range(256):
        cur = [x[linearOutput] for x in offset]
        linearInput.append(cur.index(max(cur)))


def calcOffset(pt, ct, j, guessed_key):  # 猜测第j段子密钥
    pt = list(unhexlify(pt))
    ct = list(unhexlify(ct))
    ct[j] ^= guessed_key
    ct[j] = sbox[ct[j]] # sbox即为sboxi的逆
    ct[j] = (ct[j] * coef[j]) % 256
    u1 = bitxor(pt[0], linearInput[1 << ((6 - j) % 8)])
    u2 = bitxor(ct[j], 0b10000000)
    if u1 == u2:
        return True
    else:
        return False


def linearAttack():
    key2 = []
    for i in range(8): # 第二轮子密钥的第i段
        count = [0 for _ in range(256)]
        for guessed_key in range(256):
            print("[+] Cracking key...({}-{})".format(i, guessed_key))
            for j in range(10000):
                if calcOffset(plain[j], cipher[j], i, guessed_key) == True:
                    count[guessed_key] += 1
        bias = [abs(x - 5000) / 10000 for x in count]
        key2.append(bias.index(max(bias)))
    return key2


def getkey(key2):
    ct = list(unhexlify(cipher[0]))
    pt = list(unhexlify(plain[0]))
    cur = doxor(ct, key2)
    cur = [sbox[x] for x in cur]
    cur = trans(cur)
    cur = [sboxi[x] for x in cur]
    key = doxor(cur, pt) + key2
    return key


def decrypt_block(ct, key):
    cur = doxor(ct, key[SZ:])
    cur = [sbox[x] for x in cur]
    cur = trans(cur)
    cur = [sboxi[x] for x in cur]
    cur = doxor(cur, key[:SZ])
    return cur


def decrypt(ct, key):
    pt = b''
    for i in range(0, len(ct), SZ * 2):
        block_ct = list(unhexlify(ct[i : i + SZ * 2]))
        block_pt = decrypt_block(block_ct, key)
        pt += bytes(block_pt)
    return pt


if __name__ == "__main__":
    getData(sys.argv[1], sys.argv[2])
    linearSbox()
    key2 = linearAttack()
    key = getkey(key2)
    print(key)
    flag = decrypt(enc_flag, key)
    print(flag)

在轮次高的时候，线性分析的分析复杂度往往会更高，而且成功率有所降低，具体视题目而定

中间相遇攻击

Theorem

以下基本原理参照ctf-wiki

假设 E 和 D 分别是加密函数和解密函数，$k_{1}$ 和 $k_2$ 分别是两次加密使用的密钥，则我们有

$C=E_{k_2}(E_{k_1}(P))\\ P=D_{k_2}(D_{k_1}(C))$

暴力枚举$(k_{1},k_{2})$的组合对应时间复杂度为$O(N^{2})$，而基于$E_{k_1}(P)=D_{k_2}(C)$这一事实

我们可以将$E_{k_1}(P)$和$D_{k_2}(C)$制成两张容量均为N的映射表，取交集即可获得中间态，进而恢复出两轮密钥

最好不要在求解第二张映射表的同时查表（这会使得查找耗费的时间大大增加），以两张完整表取交集即可

2020-BBCTF的经典例子:

key1 = '0'*13 + ''.join([random.choice(printable) for _ in range(3)])
key2 = ''.join([random.choice(printable) for _ in range(3)]) + '0'*13

cipher1 = AES.new(key=key1, mode=AES.MODE_ECB)
cipher2 = AES.new(key=key2, mode=AES.MODE_ECB)

print "\nGive me a string:"
pt = raw_input()

val = len(pt) % 16
if not val == 0:
    pt += '0'*(16 - val)

c1 = cipher1.encrypt(pt.encode('hex'))
c2 = cipher2.encrypt(c1.encode('hex'))
print 'Encrypted string:\n' + c2.encode('hex')

with open("flag.txt") as f:
    flag = f.read().strip()
# length of flag is a multiple of 16
ct1 = cipher1.encrypt(flag.encode('hex'))
ct2 = cipher2.encrypt(ct1.encode('hex'))
print '\nEncrypted Flag:\n' + ct2.encode('hex') + '\n'

采用中间相遇攻击即可将时间复杂度控制在$O(2\cdot 100^{3})$下

exp

# In[27]:
from Crypto.Cipher import AES
from binascii import hexlify, unhexlify
import itertools, string

# In[37]:
crack_range = list(itertools.product(string.printable, string.printable, string.printable))

# In[50]:
pt = hexlify(b'aaaaaaaaaaaaaaaa')
key_known = '0' * 13
c1 = []
cnt = 0
for suffix in crack_range:
    if not cnt % 100:
        print("\r{}/1000000".format(cnt), end="")
    key1 = (key_known + (''.join(suffix))).encode()
    cipher1 = AES.new(key1, AES.MODE_ECB)
    c1.append(cipher1.encrypt(pt))
    cnt += 1
    
# In[51]
c1 = [hexlify(c) for c in c1]

# In[54]
c1_set = set(c1)
c2 = unhexlify(b'ef92fab38516aa95fdc53c2eb7e8fe1d5e12288fdc9d026e30469f38ca87c305ef92fab38516aa95fdc53c2eb7e8fe1d5e12288fdc9d026e30469f38ca87c305')
inv_c1 = []
cnt = 0
for prefix in crack_range:
    if not cnt % 100:
        print("\r{}/1000000".format(cnt), end="")
    key2 = ((''.join(prefix)) + key_known).encode()
    cipher2 = AES.new(key2, AES.MODE_ECB)
    inv_c1.append(cipher2.decrypt(c2))
    cnt += 1
    
# In[78]
inv_c1_set = set(inv_c1)
mid_cipher = list(c1_set & inv_c1_set)[0]
key1_pos = c1.index(mid_cipher)
key2_pos = inv_c1.index(mid_cipher)
key1 = (key_known + (''.join(crack_range[key1_pos]))).encode()
key2 = ((''.join(crack_range[key2_pos])) + key_known).encode()
cipher1 = AES.new(key1, AES.MODE_ECB)
cipher2 = AES.new(key2, AES.MODE_ECB)

# In[78]
cipher = unhexlify(b'fa364f11360cef2550bd9426948af22919f8bdf4903ee561ba3d9b9c7daba4e759268b5b5b4ea2589af3cf4abe6f9ae7e33c84e73a9c1630a25752ad2a984abfbbfaca24f7c0b4313e87e396f2bf5ae56ee99bb03c2ffdf67072e1dc98f9ef691db700d73f85f57ebd84f5c1711a28d1a50787d6e1b5e726bc50db5a3694f576')
flag = unhexlify(cipher1.decrypt(unhexlify(cipher2.decrypt(cipher))))
flag

# Out[79]
b'flag{y0u_m@d3_i7_t0_7h3_m1dddl3}'

差分分析

Theorem-0

差分分析基本思想：选择大量的候选明文差分对，对应密文差分的影响来恢复尽可能多的密钥. 差分$\Delta X_{i}=X_{i}\oplus X_{i}^{*}$.

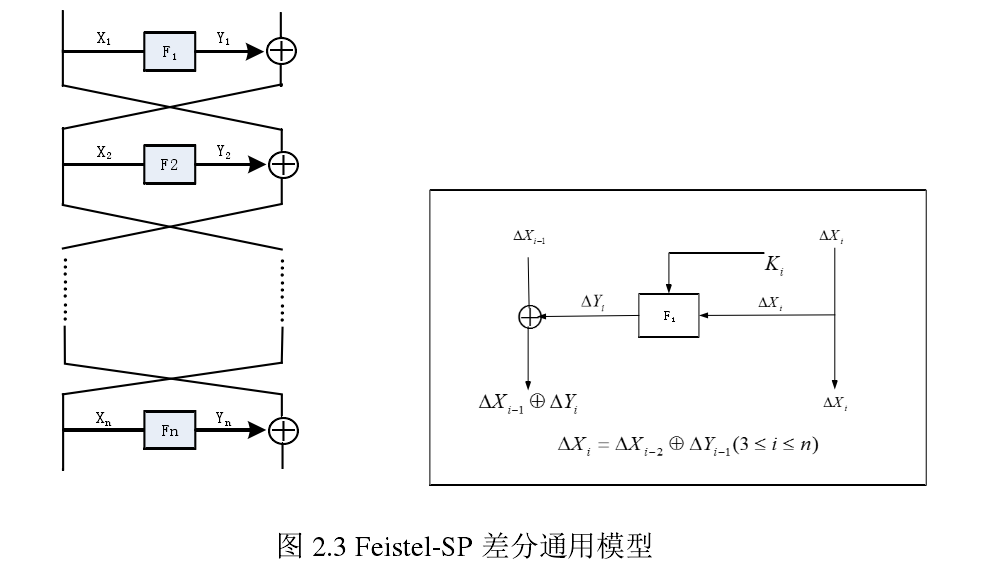
差分分析符号定义如下：

$(\Delta X_{i},\Delta Y_{i}):=Prob\{F_{i}(X_{i}\oplus\Delta X_{i},K_{i})=F_{i}(X_{i},K_{i})\oplus\Delta Y_{i}\}\\ [p_{1},p_{2},...p_{t}]=\prod_{i=1}^{t}p_{i}\\ B_{n}:=max_{\Delta X_{i}=\Delta X_{i-2}\oplus\Delta Y_{i-1}(3\leq i\leq n)}[(\Delta X_{1},\Delta Y_{1}),(\Delta X_{2},\Delta Y_{2}),...,(\Delta X_{n},\Delta Y_{n})]$

Theorem-1

下介绍如何高效搜索Feistel-SP结构分组密码的多轮高概率差分路径.

Matsui的原算法如下：

Matsui’s algorithm works by induction on the number of rounds and derives the best n-round weight B_n from the knowledge of all i-round best weight B_i (1 ≤ i ≤ n-1).

且原始的递归深搜算法复杂度相对高，因此在其基础上进行剪枝.

重构S盒差分分布表，将其转化为密集型哈希表。python用字典实现即可(输入差分→输出差分→概率)
基于向量剪枝的优化Matsui算法

在基于字节剪枝的Matsui算法中，频繁的穷尽搜索$2^{32}$或$2^{64}$，因此使用向量递归调用，尽可能早的过滤不满足的$\Delta X_{i}$和$\Delta Y_{i}$.

以下是对Round-2的算法剪枝，后续轮也可采用相似算法
1
2
Call Procedure Round-2-1
Return to the upper procedure.
Procedure Round-2-j (1 <= j <= 8):

For each candidate for $\Delta X_{2}^{j}$ and $\Delta Y_{2}^{j}$,do:
- $\quad p_{2}^{j} = (\Delta X_{2}^{j}, \Delta Y_{2}^{j})$ and $p_{2} = [p_{2}^{1}, …, p_{2}^{j}]$;
- $\quad if\ [p_{1}, p_{2}, B_{n-2}]< \bar{B_{n}}$, then continue;
- $\quad if\ [p_{1}, p_{2}, B_{n-2}]\geq \bar {B_{n}}$:
  
  if $j\neq 8$, then call Procedure Round-2-(j+1);
  
  else call Procedure Round-3;

Theorem-2

差分过程可以简单归纳为

(1) 采样：选择大量合适的明文对(满足差分)，并获得相应的密文对；

(2) 去噪，通过观察密文对差分的一些特性，提早过滤一部分不正确的明文对，排除干扰；

(3) 提取信息，对过滤后的数据和每个猜测密钥进行统计分析，恢复正确轮密钥(部分比特)；

m: 样本量大小; p: 差分区分器概率; $\upsilon$: 平均每个密文对蕴含的密钥数;

l: 攻击所猜测的密钥量; $\lambda$: 去噪阶段的过滤系数

注：其中$\upsilon$与S盒差分分布表有关，大致估计方法可以为：

(e.g.) S盒6进4出，平均意义上差分分布表的取值为$2^{6}/2^{4}=4$. 假设一次攻击猜测4个S盒对应的密钥，则该参数可估计为$4^{4}=2^{8}$.

则正确密钥至少被统计了$mp$次，所有猜测密钥平均被统计了$\frac{m\lambda\upsilon}{2^{l}}$次，则信噪比

$S/N=\frac{mp}{m\lambda\upsilon/2^{l}}=\frac{p\cdot 2^{l}}{\lambda\upsilon}.$

信噪比越大，即正确密钥被统计次数相对越多，更容易在计数器中被区分，从而降低选择明文攻击的明文量

$m\approx \frac{c}{p},c=constant$. 以Shamir提出的DES相关实验数据为例：

$S/N\in [1,2]$，c取值$[20,40]$；$S/N$更大时，c取值$[3,4]$.

Theorem-3

对n轮Feistel的差分攻击，一般性上往往是1-R攻击，至于m-R攻击（如对八轮DES的3-R差分攻击），尽管差分特征概率会有所降低，但往往需要根据具体S盒P盒进行更特殊的构造，而非直接利用搜索到的n-1轮高概率差分特征进行攻击。

且对于非双射关系的S盒（如DES六进四出的S盒），即可能存在两轮迭代差分特征，如下图所示：

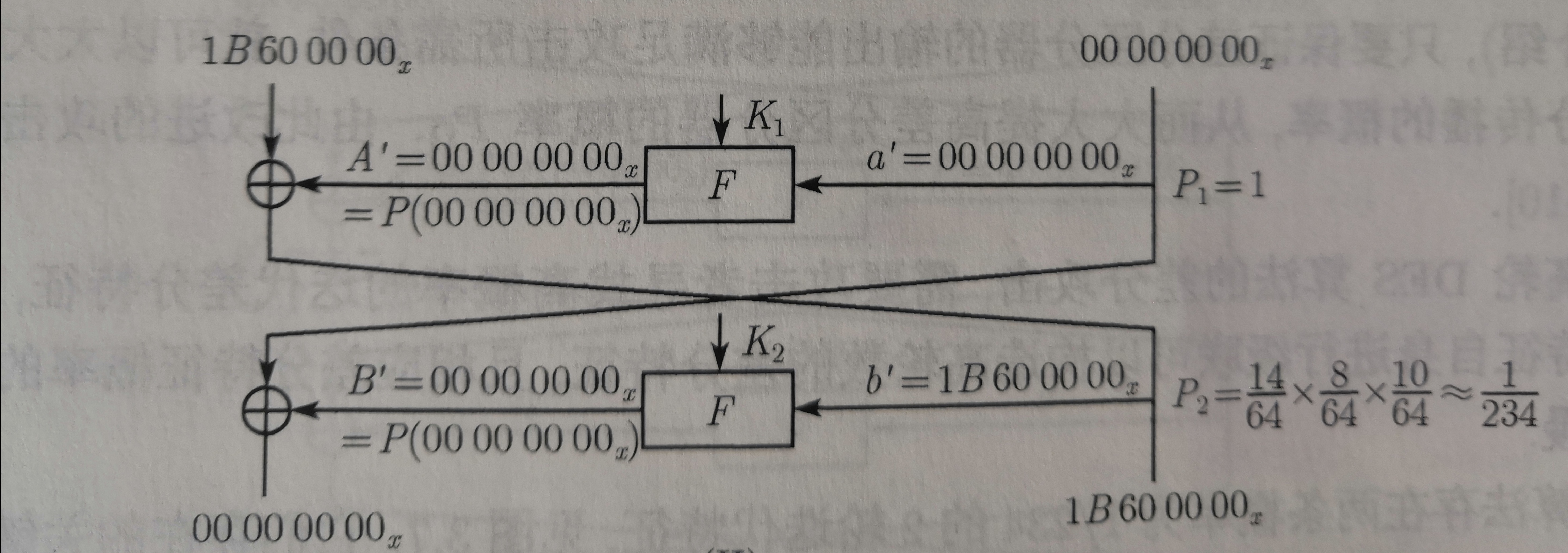
因为该类的S盒存在输入差分不为0，但输出差分为0的情况，在Pro(in, 0)较大时，我们就能利用二轮迭代差分特征实现2n+1(n>=1)轮Feistel的1-R攻击（完全依赖于S盒特性及相邻S盒间关系）

搜索仅sbox[i]~sbox[j]激活的二轮迭代差分特征可采用以下递归算法实现（以下算法基于DES的E函数（F函数第一步）扩展）

# 2-round iterative differential feature (sbox[i]~sbox[j])
def find_path(pre, i, j):
    global dif_dist
    sub_pro = 1
    max_pro = sub_pro
    cur_path, path = None, []
    for key in dif_dist[i].keys():
        if key[1] == 0 and ((key[0] & 0b110000) >> 4) == (pre & 0b000011):
            if i == j and (key[0] & 0b000011) != 0:
                continue
            value = dif_dist[i][key]
            if value % 64 == 0:
                continue
            if i < j:
                path, sub_pro = find_path(key[0], i + 1, j)
            if value * sub_pro > max_pro:
                max_pro = value * sub_pro
                cur_path = [key[0]] + path
    if not cur_path:
        return None, 0
    else:
        return cur_path, max_pro # pro = max_pro / (64 ** (j - i + 1))

exp

以WMCTF出的idiot box为例，我的本意是S盒随机shuffle生成，key不变，动态请求靶机直至找到使高概率二轮迭代差分特征存在的S盒，但阿里云频繁remote真的慢慢慢慢慢慢，还会被banip

version1的exp是一次攻击两个相邻S盒，分四段得到第六轮的子密钥，但是因为上述原因改了- -

改成静态S盒后，又有一样的问题，拿差分攻击要的明密文对本地秒出，但是docker挂载阿里云以后发现取$2^{12}$个明文对都要三分钟- -NM$L

于是version1的exp因为每段要取$2^{14}$个明文对，分四段（$2^{16}$对），改成了version2每段取$2^{12}$个明文对，分八段（$2^{15}$对）

Sbox也改成了根本就不符合S盒定义的Sbox，因为其实是不存在针对单个S盒的二轮迭代的（因为由E扩展函数知，该迭代差分特征要求输入差分为$00x_{1}x_{2}00$（即明文对处于同行），所以不可能存在满足该差分输入的明文对同时满足差分输出为0）

歪日，👴真的吐了，version1远程exp估计要跑将近1h，相较之下version2的exp将近30min，还算能接受…吧

这里给出我version1的本地测试exp，就不放WMCTF上的版本了（这个根本称不上是S盒的Sbox一直有、膈应

Click Here to Download idiot box-version 1

再做下exp里一些部分的解释：

针对相邻两个S盒的find_path：
1
while max_pro < 192: # find suitable sbox
要求max_pro < 192的原因是要令S/N足够大，$S/N\geq\frac{2^{12}(\frac{192}{64*64})^{2}}{4^{2}}\geq 0.5625$，因此可将c暂取为40，$m=c/p\leq 40\frac{64^{4}}{192^{2}}\approx 18204$，所以
1
2
3
for i in tqdm(range(2**(4*(right-left+1)))):
for j in range(2**3):
for k in range(2**3):
每次取$2^{14}$个明文对，并同时通过密文右半部分差分过滤错误对

关于选择明文攻击时明文shift的解释：

1
2
3

i_shift = 60 - right * 4
j_shift = (i_shift - 3) % 32 + 32
k_shift = (i_shift + 4 * (right - left + 1)) % 32 + 32

选取的明文对注意一定要激活差分特征上的活跃S盒

密钥计数器得到的最后一轮候选子密钥可能存在多解，验证校验明文即可

滑动攻击

Theorem

https://0xdktb.top/2020/09/22/%E9%87%91%E8%9E%8D%E5%AF%86%E7%A0%81%E6%9D%AF2020-%E6%8C%91%E6%88%98%E8%B5%9B/

http://theamazingking.com/crypto-slide.php

Group Mode(ECB)

Theorem

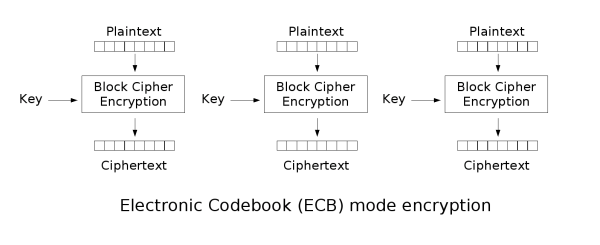
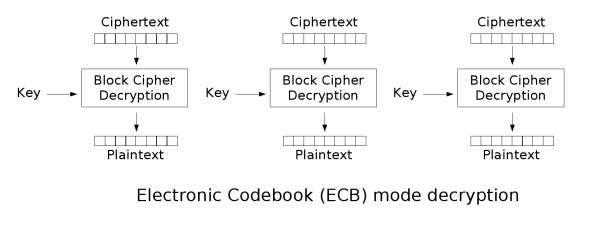
以i春秋2020公益赛NewsWebsite为例：

@Value("${system.encrypt_key}")
private String signKey;
@Value("${system.flag}")
private String sign;
  
private String desEncrypt(String plainText)
{
  String cipher = "";
  byte[] originPlainText = (plainText + System.currentTimeMillis() + this.sign).getBytes();
  try
  {
    TripleDesCipher tripleDesCipher = new TripleDesCipher(this.signKey.getBytes());
    cipher = Base64.getEncoder().encodeToString(tripleDesCipher.encode(originPlainText));
  }
...

其3DES有选择明文攻击，且plainText可控，返回的密文为$E_{k}(plainText+System.currentTimeMillis()+flag)$

currentTimeMillis返回长度固定（除非运气极差碰上最高位进位…想peach）

且有private static String TRIPLE_DES_TRANSFORMATION = "DESede/ECB/PKCS5Padding"，因此有如下攻击方法：

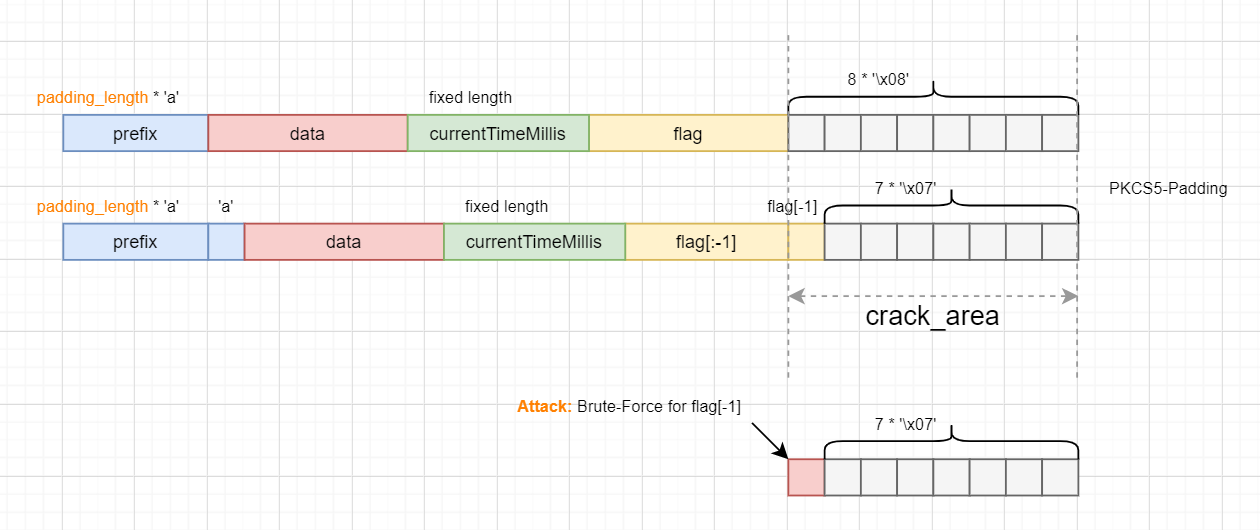
prefix填充padding_length*'a'后，恰好能使PKCS5后最后为8*'\x00'

基于$8\mid(len(E_{k}(‘’+currentTimeMillis+flag))+padding_length)$

得到crack_area分组对应密文后，由于crack_area明文段后7bits均已知，因此send data为爆破位+7已知bits，当返回的ct[:8]与前者吻合时，爆破当前比特位成功

后续比特位均类似，prefix++得到新的crack_area内容，进而逐位爆破即可

exp

import requests
from base64 import b64decode
import string

url1 = "http://dcf1d021-491b-4279-ae42-d56a10fc3334.node3.buuoj.cn/api//comment/news/28"
url2 = "http://dcf1d021-491b-4279-ae42-d56a10fc3334.node3.buuoj.cn/api//comment/news/28?size=10&page=0&sort=commentId%2Cdesc"

def web_encrypt(payload):
    r = requests.post(url1, json={"commentEmail": "1@qq.com",
                                  "commentContent": payload, "commentNickname": "0xDktb"})
    commentId = r.json()['commentId']
    r = requests.get(url2)
    content = r.json()['content']
    for _ in content:
        if _['commentId'] == commentId:
            return b64decode(_['commentContent'])

def crack_padding_length():
    origin_length = len(web_encrypt(''))
    for i in range(1, 9):
        cur_length = len(web_encrypt('a' * i))
        if cur_length != origin_length:
            return (i, cur_length)  # 8 | (len(enc(salt)) + i)

def crack_salt(padding_length, crack_pos):
    salt = ''
    for i in range(42):
        crack_area = web_encrypt(
            'a' * (len(salt) + padding_length + 1))[crack_pos-8:crack_pos]
        if len(salt) >= 7:
            payload = salt[:7]
        else:
            payload = salt + (7 - len(salt)) * chr(7 - len(salt))
        isFound = False
        for c in string.printable:
            guess = web_encrypt(c + payload)[:8]
            if guess == crack_area:
                isFound = True
                salt = c + salt
                break
        assert(isFound == True)
        print(salt)

def main():
    padding_length, crack_pos = crack_padding_length()
    crack_salt(padding_length, crack_pos)

if __name__ == "__main__":
    main()

Group Mode(CBC)

Theorem

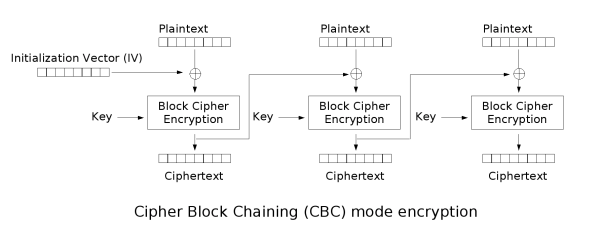
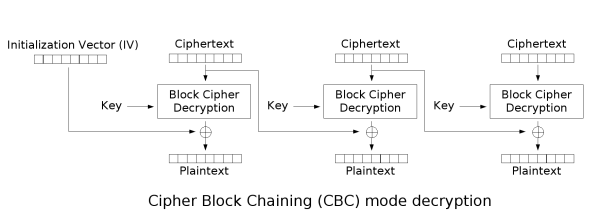
CBC - Flipped Ciphertext Bits

可以看到CBC模式下，任一分组$C_{i}$的解密结果，均只与$C_{i}$和$C_{i-1}$有关（$C_{1}$只和$IV,C_{1}$有关）

因此只需令$C_{i-1}=C_{i-1}\oplus P_{i}\oplus (you\ want)$即可（从最后一块向前翻转）

In [1]: import os
   ...: from Crypto.Cipher import AES
   ...: key, iv = os.urandom(16), os.urandom(16)
   ...: aes1 = AES.new(key, AES.MODE_CBC, iv)
   ...: aes2 = AES.new(key, AES.MODE_CBC, iv)

In [2]: pt = b"0xDktb_wants_a_girlfriend_orzzzzzzzzzzzzzzzzzzzzzzzzzzzz"
   ...: pad = lambda x : (x + (16 - len(x) % 16) * bytes([16 - len(x) % 16]))
   ...: pt = pad(pt)
   ...: len(pt)
Out[2]: 64

In [3]: def xor(a, b):
   ...:     return bytes(x ^ y for x, y in zip(a, b))
   ...: ct = aes1.encrypt(pt)
   ...: payload = b"pt_1st_1s_H3r3!!pt_2nd_1s_H3r3!!pt_3rd_1s_H3r3!!pt_4th_1s_H3r3!!"

In [4]: for i in range(3):
   ...:     ct_block = xor(xor(pt[16*(3-i):16*(4-i)], ct[16*(2-i):16*(3-i)]), payload[16*(3-i):16*(4-i)])
   ...:     ct = ct[:16*(2-i)] + ct_block + ct[16*(3-i):]
   ...:     dec_iv = ct[-16:]
   ...:     pt = aes2.decrypt(ct)
   ...: dec_iv = xor(xor(pt[:16], dec_iv), payload[:16])
   ...: aes3 = AES.new(key, AES.MODE_CBC, dec_iv)
   ...: pt = aes3.decrypt(ct)
   ...: print(pt)
b'pt_1st_1s_H3r3!!pt_2nd_1s_H3r3!!pt_3rd_1s_H3r3!!pt_4th_1s_H3r3!!'

CBC - Chosen Plaintext Attack

https://0xdktb.top/2020/08/02/WriteUp-WMCTF2020-Crypto/#Game

CBC - Padding Oracle Attack

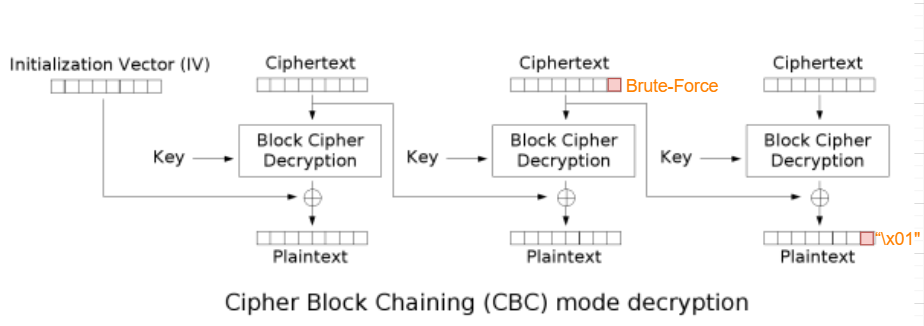
在服务器检查解密合法性，为检查PKCS5-padding的suffix部分，且合法与非法返回不同状态时（不返回明文内容），可以采用Padding Oracle Attack

Group Mode(GCM)

Theorem0

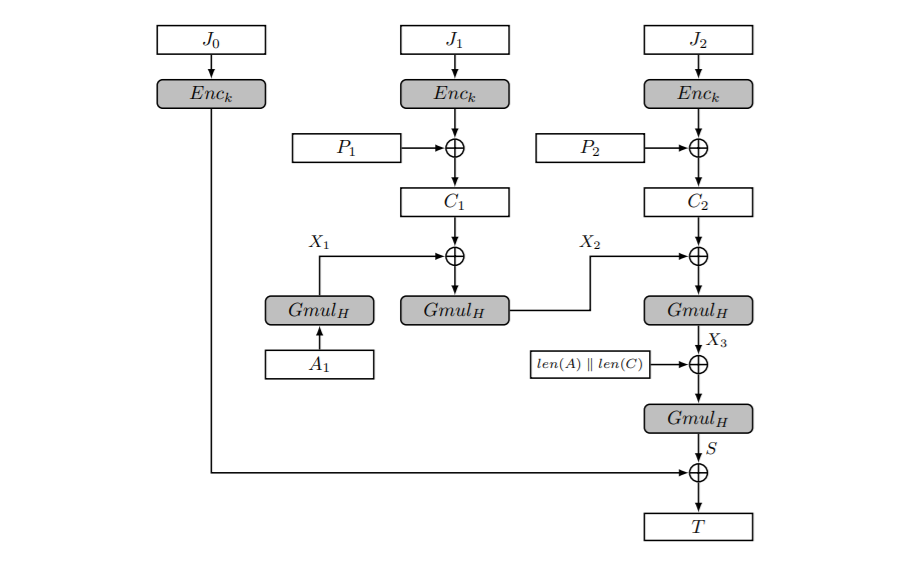
对AES-GCM，有以下符号定义：

$a|b$: a, b位串的连接；

$0^{s}$: 长度为s的0串

$A_{i}$: 第i块的auth-data

$IV$: 96bits(12bytes)初始向量

$cnt$: 4bytes计数器counter值，$cnt=(i+1)\%2^{32}$

$J_{i}$: 第i块的Enc input，$J_{0}=IV||0^{31}||1$

$Gmul_{H}(X)$: $GF(2^{128})$上的$H\cdot X$，素多项式$f=1+\alpha+\alpha^{2}+\alpha^{7}+\alpha^{128}$

对生成auth-tag的过程有：

$H=Enc_{k}(0^{128})$
$X_{0}=0$，假设Auth-data占了m个block长度，$X_{i}=Gmul_{H}(X_{i-1}\oplus A_{i})$,for $i\in\{1,..,m\}$
$X_{i+m}=Gmul_{H}(X_{i+m-1}\oplus C_{i})$,for $i\in\{1,…,n\}$
$S=Gmul_{H}(X_{m+n}\oplus(len(A)||len(C)))$，len(A)和len(C)均为长度64的位串（BLOCK_SIZE/2)
$T=S\oplus Enc_{k}(J_{0})$，即为auth-tag

GCM最后返回的消息为$C||T$.

Theorem1 - The Forbidden Attack

Overview

TLS下的AES-GCM生成的12bytes IV由以下部分组成：

Salt(4 bytes)：由TLS handshake，值等于server_write_IV / client_write_IV，属于IV的implicit part
Nonce(8 bytes)：服务器随机生成，属于IV的explicit part

$g(X)=A_{1}X^{m+n+1}+…+A_{m}X^{n+2}+C_{1}X^{n+1}+…+C_{n}X^{2}+LX+Enc_{k}(J_{0})$

(其中$L=(len(A)||len(C))$)

$g(H)=T$

我们的攻击主要基于已找到Nonce相同的一对collision（同一会话下Salt不变），则有

假设$m=0,n=1$，

$g_{1}(X)=C_{1,1}X^{2}+L_{1}X+Enc_{k}(J_{0})$

$g_{2}(X)=C_{2,1}X^{2}+L_{2}X+Enc_{k}(J_{0})$

且$g_{1}(H)=T_{1},g_{2}(H)=T_{2}$

$\therefore(C_{1,1}+C_{2,1})H^{2}+(L_{1}+L_{2})H+T_{1}+T_{2}=0$. (系数均已知)

故candidate H在上述方程的roots中，而roots总数一般与方程degree相同，且现实中degree并不会过大（消息极长除外），因此在发生nonce collision时，H的值就能被攻击

有了H就意味着我们能自生成合法auth-tag

攻击场景实例：

服务器与客户端间以AES/GCM进行通信，AES密钥及4bytes的Salt双方在通过密钥协商协议后各自保存在本地（第三方无法获取）

在正常通信时，传输的为cipher & auth-tag T & Nonce(8 bytes)，可被第三方截取

则若我们通过上述方法攻破H，又有已知明文攻击的Oracle，即可通过已知明文的一组数据进行密文篡改并自生成合法auth-tag，实现对服务器的欺骗

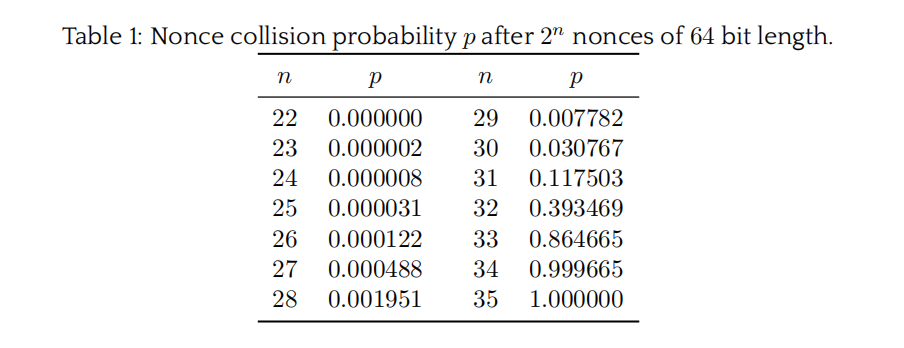
Group Mode(CTR)

Theorem0

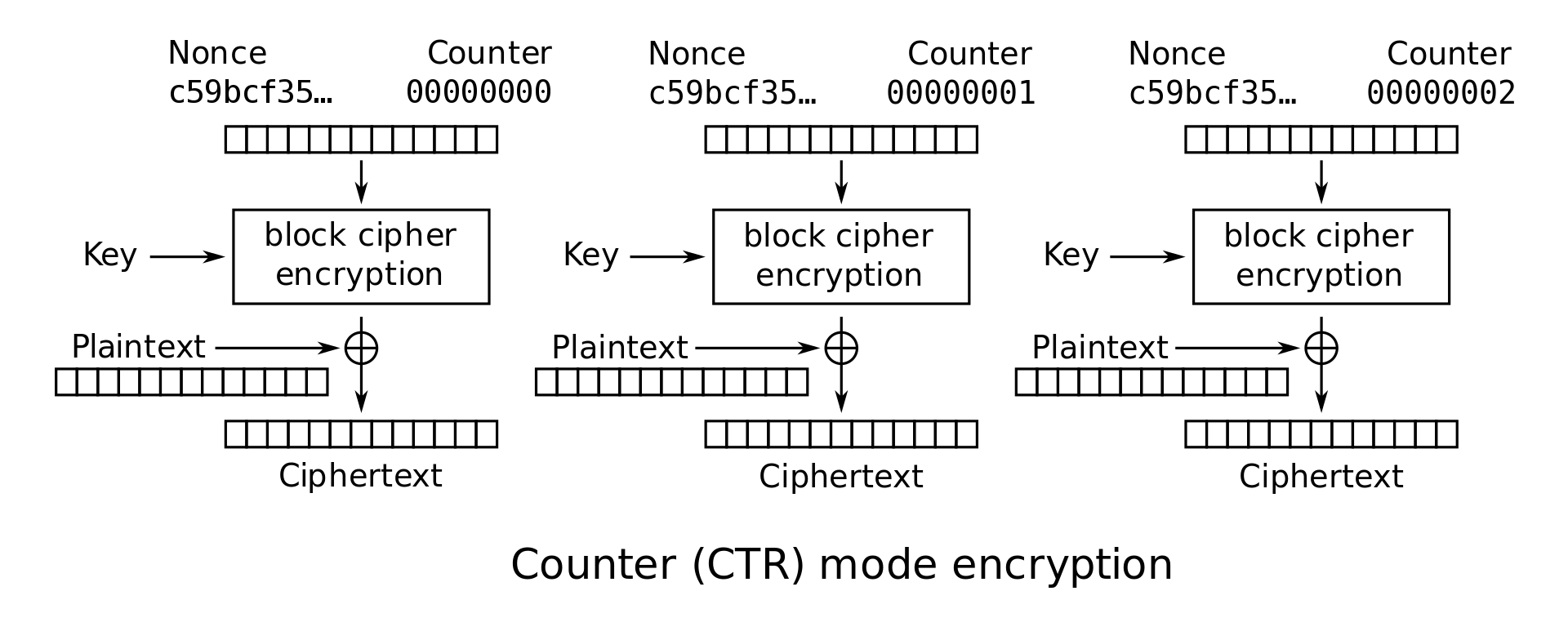
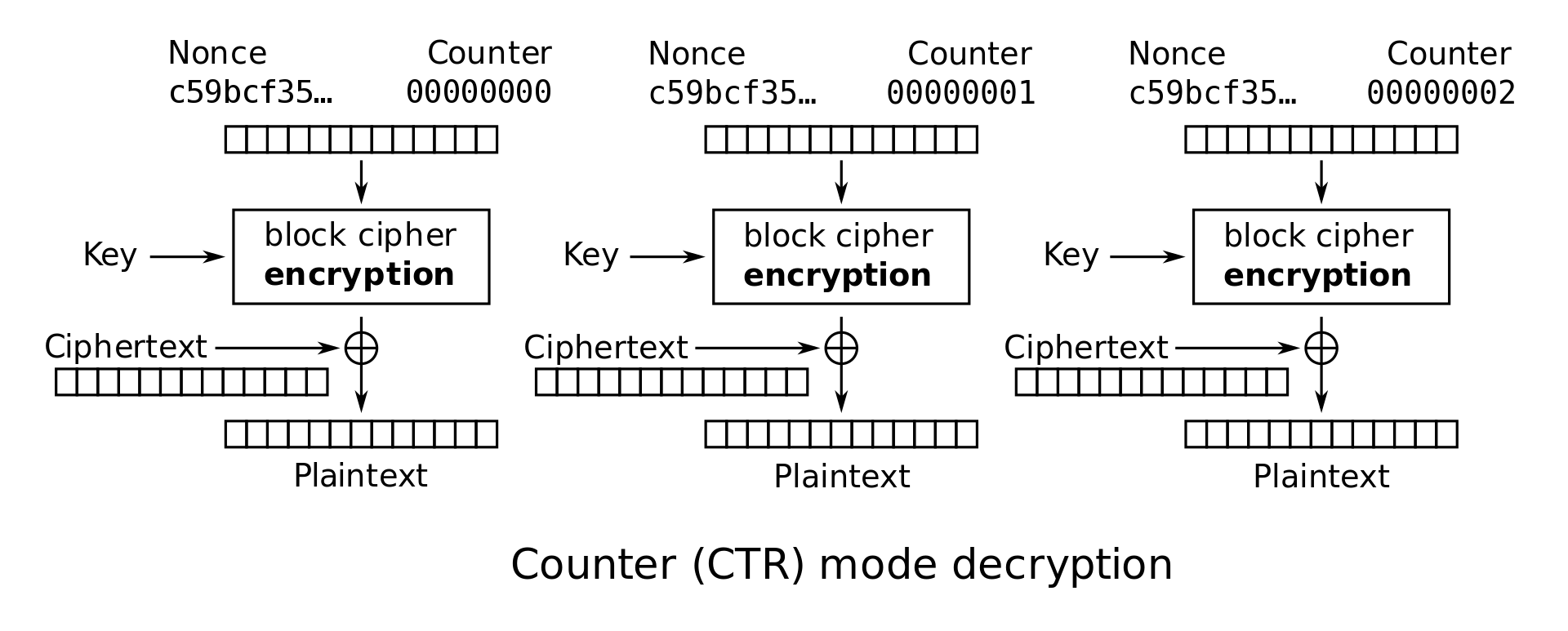
$C_j=E_k(nonce_j)\oplus P_j$

$P_j=E_k(nonce_j)\oplus C_{j}$

Theorem1 - Separator Oracle

假设明文格式为$username||timestamp||userlevel$

Separator Oracle能应用的场景大致为：

普通用户注册后，服务器给出其$username||timestamp||userlevel$通过CTR加密生成的token，保持作sessionid

在发起登陆请求时，服务端解密sessionid后若不成功会根据具体情况返回不用Exception

我们主要利用的为separate错误引起的Error抛出：

separator = '|'
ct = get_cookie('sessionid')
pt = decrypt(ct)
pt = pt.split(separator)
if len(pt) != 3:
    raise ValueError("Separate failed.")

攻击思路如下：

pt = [0] * len(ct)
for i in range(len(ct)):
    new_ct1 = ct[:i] + bytes([ct[i] ^ 1]) + ct[i+1:]
    new_ct2 = ct[:i] + bytes([ct[i] ^ 2]) + ct[i+1:]
    resp1, resp2 = oracle(new_ct1), oracle(new_ct2)
    if resp1 == SeparatorException and resp2 == SeparatorException:
        pt[i] = ord('|') # i is a separator's index
    else:
        for j in range(1, 0x100):
            new_ct = ct[:i] + bytes([ct[i] ^ j]) + ct[i+1:]
            resp = oracle(new_ct)
            if resp == SeparatorException: # add a separator(too much)
                pt[i] = j ^ ord('|')
                break
pt = bytes(pt)

def xor(a, b):
    return bytes(x ^ y for x, y in zip(a, b))

key = xor(pt, ct)

原理很简单，CTR实质上可视作流密码（因为在需要加解密时，其分组密码部分得到的key是固定的）

对于ct的任一byte，若其对应pt的byte为一separator，则在异或上任一非零值送去解密时，oracle均会返回SeparatorException（occurred by removing a separator）

而若对应的非separator，则只需爆破异或的值，当返回SeparatorException时，即可知$new_ct\oplus j=ct\oplus ord(‘|’)$

通过这种攻击方式，我们能还原出分组加密部分的Key，且由于CTR mode是没有鉴别码机制的

因此我们能得到任意P’对应的密文$C’=C\oplus P\oplus P’$，即合法token，进行admin伪造（若中间为时间戳的话需篡改为满足token现仍有效期内的值）

高阶差分分析

Theorem0 - 离散高阶函数与高阶差分

定义1. 设$(S,+)$和$(T,+)$是两个Abel群，$f:S\rightarrow T$，则f在S中a点处的导数定义为

$\Delta_{a}f(x)=f(x+a)-f(x)$

在点$\{a_1,a_2,…,a_i\}$处的i阶导数定义为

$\Delta_{a_1,a_2,...,a_i}^{(i)}f(x)=\Delta_{a_i}(\Delta_{a_1,a_2,...,a_i}^{(i-1)}f(x))$

命题1. 设f是一个n变元的布尔函数，函数的代数次数为deg(f)，则

$deg(\Delta_af(x))\leq deg(f(x))-1$

(布尔函数f是从$F_2^n$到$F_2$的映射)

命题2. 设f是一个n变元的布尔函数，则函数的n阶导数为常数(constant)，进一步，若f可逆，则其n-1阶导数为常数

命题3. 设f是一个n变元的布尔函数，$L[a_1,…,a_i]$是$a_1,…,a_i$的所有可能的线性组合，则

$\Delta_{a_1,...,a_i}^{(i)}f(x)=\sum_{c\in L[a_1,...,a_i]}f(x\oplus c)$

命题4. 布尔函数的高阶导数只依赖于其阶的大小，即

$\Delta_{a_1,...,a_i}^{(i)}f(x)=\Delta_{a_{\pi(1)},...,a_{\pi(i)}}^{(i)}f(x)$

命题5. 设$f:F_2^n\rightarrow F_2^n$，$a_1,a_2,…,a_i$是$F_2^n$上i个线性无关的向量，若x在$F_2^n$上分布均匀，则对任意$b\in F_2^n$，等式$\Delta_{a_1,…,a_i}^{(i)}f(x)=b$成立的概率要么为0，要么至少为$2^{i-n}$

Proof: 假设有$\Delta_{a_1,…,a_i}^{(i)}f(x_0)=b$，则$\sum_{c\in L[a_1,…,a_i]}f(x\oplus c)=b$，进而

$\forall c\in L[a_1,…,a_i],\Delta_{a_1,…,a_i}^{(i)}f(x_0\oplus c)=b$，$Pro(\Delta_{a_1,…,a_i}^{(i)}f(x)=b)\geq2^{i}/2^{n}=2^{i-n}$

Q.E.D.

命题6. 当输入x均匀时，则差分对(a, b)出现的概率为f(x)在点a处的一阶导数取值b的概率

$P(\Delta_y=b|\Delta_x=a)=P(f(x+a)-f(x)=b)=P(\Delta_af(x)=b)$

进而推广至高阶差分，函数的一条i阶差分，即找到一i+1元数组$(a_1,…,a_i,b)$，使得$\Delta_{a_1,…,a_i}^{(i)}f(x)=b$

离散高阶函数与高阶差分的联系为： f(x)有一条i阶差分$(a_1,…,a_i,b)$当且仅当f(x)在$(a_1,…,a_i)$处导数为b

Theorem1 - 高阶差分攻击

以下为对一般分组密码的高阶差分攻击的框架：

设E是一个r rounds的分组密码算法，可写作$Y=E(X,K)$，假设

r-1 rounds的加密算法$E_{r-1}(X,K_{1},…,K_{r-1})$的deg为d，则

$\Delta_{a_1,...,a_d}^{(d)}E_{r-1}(X,K_{1},...,K_{r-1})=0$

(由于$E_{r-1}$可逆)，且有

$E_{r}^{-1}(Y,K_{r})=E_{r-1}(X,K_{1},...,K_{r-1})\\ \Delta_{a_1,...,a_d}^{(d)}E_{r}^{-1}(Y,K_{r})=0\\ \therefore\sum_{c\in L(...)}E_{r}^{-1}(Y\oplus c,K_{r})=0$

则当d-1足够小时，攻击者就可以通过下述攻击流程获得最后一轮的轮密钥$K_{r}$：

寻找一个r-1 rounds的高阶差分区分器；
根据差分区分器的输出特征，确定要恢复的最后一轮轮密钥长度（一般不直接一次性恢复完整长度的轮密钥），不妨设所要恢复的部分轮密钥长度为s，则设置$2^{s}$个密钥计数器，初始化均为0；
随机选取一个d维子空间L（要求E可逆），则对所有$X\in L$，利用同一未知的密钥对其进行加密，获得对应的密文Y（Chosen Plain Attack，Oracle）；
利用所有最后一轮的候选密钥对Y进行解密并求和，若该值为0，则对应counter++；
选取counter max对应的作为正确$K_{r}$；

Feistel-SP结构

线性分析

Theorem

exp

More

中间相遇攻击

Theorem

exp

差分分析

Theorem-0

Theorem-1

Theorem-2

Theorem-3

exp

滑动攻击

Theorem

Group Mode(ECB)

Theorem

exp

Group Mode(CBC)

Theorem

CBC - Flipped Ciphertext Bits

CBC - Chosen Plaintext Attack

CBC - Padding Oracle Attack

Group Mode(GCM)

Theorem0

Theorem1 - The Forbidden Attack

Overview

Group Mode(CTR)

Theorem0

Theorem1 - Separator Oracle

高阶差分分析

Theorem0 - 离散高阶函数与高阶差分

Theorem1 - 高阶差分攻击