WriteUp(De1CTF2020) - Crypto

NLFSR

[题解分析]

分析源码发现是四个LFSR组合成的加密系统，相关系数分析如下：

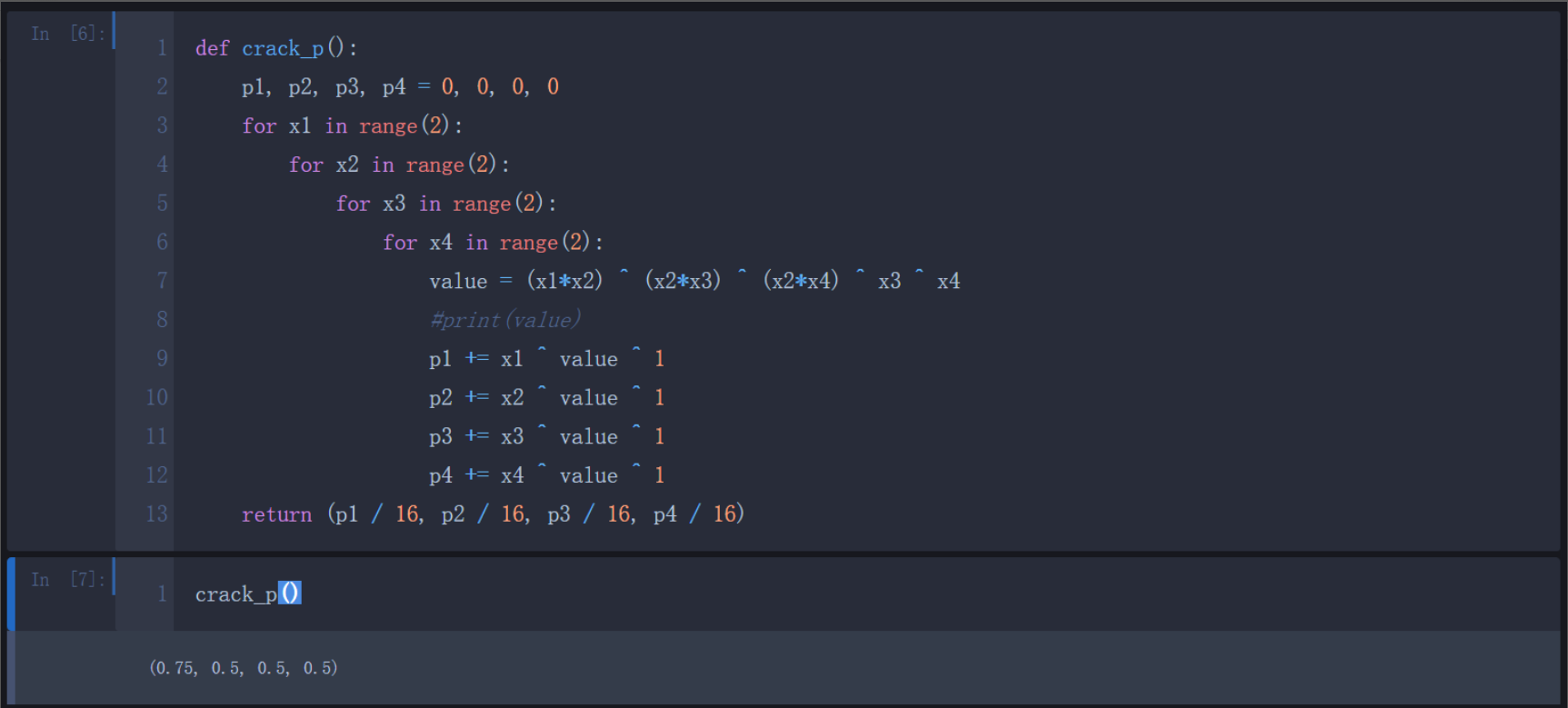
发现第一个LFSR相关系数0.75，相关攻击即可

...
def crack_key(p, mask, partMask):
    for a in range(2**18, 2**19):
        single_cipher = single_lfsr(a, mask, partMask, len(cipher))
        correlation_value = correlation(single_cipher, cipher)
        if correlation_value >= (p - 0.05) and correlation_value <= (p + 0.05):
            print("a is {}".format(a))
            return

得到 a = 363445

因为$x_{2}=0$时，$value=x_3\oplus x_4$；$x_2=1$时，$value=x_1$，所以第一个LFSR流与最终流不一致的比特位上，第二个LFSR流一定为0

取第一个LFSR流与最终流不一致的至少19个比特位，即可恢复b

single_cipher_a = single_lfsr(a, ma, partMask, len(cipher))

b0_pos = [] #b==0的下标
for i in range(2048):
    if cipher[i] != single_cipher_a[i]:
        b0_pos.append(i)
b0_pos = b0_pos[:19]
        
mb = 0x40f3f

mb_feedback = []
mb_bin = bin(mb)[2:].rjust(24, '0')
for i in range(24):
    if mb_bin[i] == '1':
        mb_feedback.append(i)
mb_feedback.append(24)
mb_feedback = [_ - 5 for _ in mb_feedback]
# mb_feedback = [0, 7, 8, 9, 10, 13, 14, 15, 16, 17, 18]

cur = []
F2 = GF(2)

for i in range(19):
    v = vector(F2, 19)
    v[i] = 1
    cur.append(v)

for i in range(100):
    v = vector(F2, 19)
    cur19 = cur[-19:]
    for j in mb_feedback:
        v += cur19[j]
    cur.append(v)
    
cur = cur[19:]

left = []
for i in b0_pos:
    left.append(list(cur[i]))
A = Matrix(F2, left)

A.right_kernel()

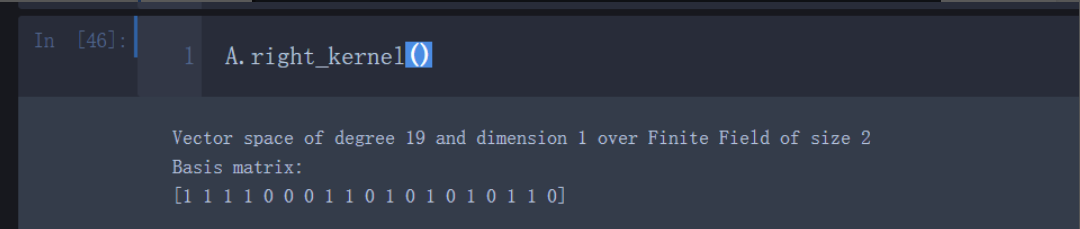
于是得到 b = 0b1111000110101010110 = 494934

最后两个LFSR组成的密钥空间$2^{19}$，直接爆破即可

得到 c = 4406，d = 63

easyRSA

[题解分析]

给出$e_{1},e_{2}$，对应的私钥满足

1
2
3

limit = gmpy2.iroot(n,3)[0]
r = random.randint(limit,limit*0x1000000000001)
d = gmpy2.next_prime(r)

2048 bits N下的这个上界(731 bits)显然不满足Wiener和Boneh Durfee，因此采用这篇paper下的攻击方法：

$g=gcd(p-1,q-1),\lambda(n)=\frac{\varphi(n)}{g},s=1-p-q$

且有$ed-k\lambda(n)=1$，得到$edg-kn=g+ks\quad (1)$

设$e_{1}$对应$k_{1}$，$e_{2}$对应$k_{2}$，则有$k_{2}d_{1}e{1}-k_{1}d_{2}e_{2}=k_{2}-k_{1}\quad (2)$

由(1)(2)有：

$\left\{ \begin{matrix} e_{1}d_{1}g-k_{1}n=g+k_{1}s\\ k_{2}d_{1}e{1}-k_{1}d_{2}e_{2}=k_{2}-k_{1}\\ e_{1}e_{2}d_{1}d_{2}g_{2}-e_{1}d_{1}gk_{2}n-e_{2}d_{2}gk_{1}n+k_{1}k_{2}n^{2}=(g+k_{1}s)(g+k_{2}s) \end{matrix} \right.$

上述等式组也可表示为

$[k_{1}k_{2},k_{2}d_{1}g,k_{1}d_{2}g,d_{1}d_{2}g^{2}]\cdot\left[ \begin{matrix} n & -M_{1}n & 0 & n^{2}\\ 0 & M_{1}e_{1} & M_{2}e_{1} & -e_{1}n\\ 0 & 0 & -M_{2}e_{2} & -e_{2}n\\ 0 & 0 & 0 & e_{1}e_{2} \end{matrix} \right]\\ =[k_{1}k_{2}n,M_{1}k_{2}(g+k_{1}s),M_{2}g(k_{2}-k_{1})，(g+k_{1}s)(g+k_{2}s)]$

(其中$M_{1}=n^{1/2},M_{2}=n^{1+\alpha_{2}},d\approx n^{\alpha_{2}}$.)

对部分参数进行上界估计，k上界近似于$d\approx N^{\alpha_{2}}$，$|s|$上界$\approx N^{1/2}$，g一般相对极小

因此上面的矩阵表示BA=C中，C的每个元的size都近似$n^{1+2\alpha_{2}}$，所以$|C|\approx 2\cdot n^{1+2\alpha_{2}}$

B作为格基的格中，最短向量由Minkowski Bounds知$\approx \sqrt{4}det(B)^{1/4}\approx 2\cdot n^{(13/2+\alpha_{2})/4}$

因此只要满足$n^{1+2\alpha_{2}}<n^{(13/2+\alpha_{2})/4}$即可将问题转化为SVP（$\alpha_{2}<\frac{5}{14}$）.

[exp]

n = 
e1 = 
e2 = 
c = 

from Crypto.Util.number import *

for i in range(731, 682, -1):
    print(i)
    alpha2 = i / 2048
    M1 = round(n ^ 0.5)
    M2 = round(n ^ (1 + alpha2))
    A = Matrix(ZZ, [
        [n, -M1*n,      0,   n^2],
        [0, M1*e1, -M2*e1, -e1*n],
        [0,     0,  M2*e2, -e2*n],
        [0,     0,      0, e1*e2]
    ])
    AL = A.LLL()
    C = Matrix(ZZ, AL[0])
    B = A.solve_left(C)[0]
    phi1 = floor(e1 * B[1] / B[0])
    phi2 = floor(e2 * B[2] / B[0])
    d1 = inverse(e1, phi1)
    d2 = inverse(e2, phi2)
    m1 = long_to_bytes(pow(c, d1, n))
    m2 = long_to_bytes(pow(c, d2, n))
    if b"De1" in m1 or b"De1" in m2:
        print(m1)
        print(m2)
        break

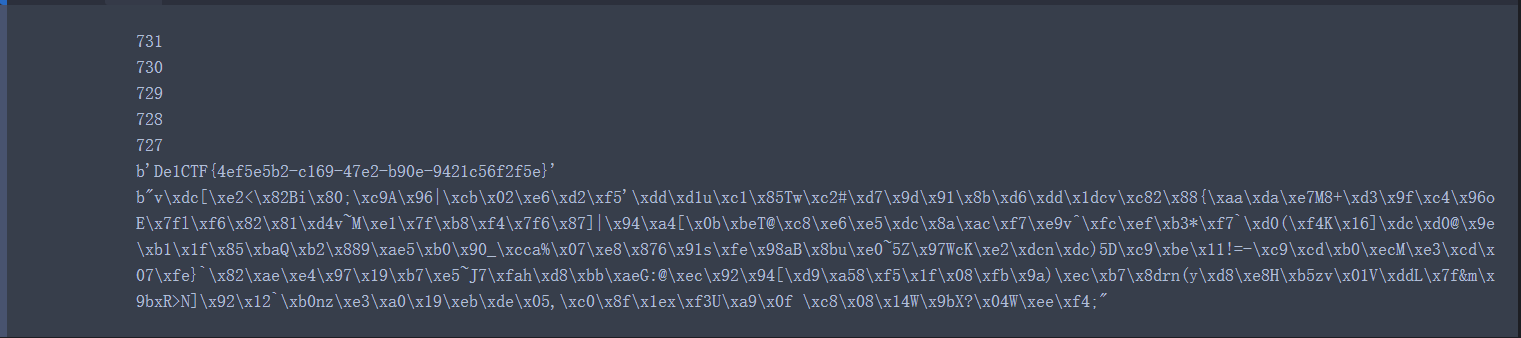
可以发现727 bits的时候LLL求解SVP成功

[More]

Day1晚上coin和我说是d3原题…只不过是size(d)只有一个范围，$\alpha_{2}$要进行调整（原理理解起来不难…还是做题太少- -

ECDH

没看-.-shallow师傅自己一个人a掉了tql

（题解分析视时间补充

Mini Purε Plus

[题解分析]

De1CTF2019也出过Purε，但那时候考察的是最基本的插值攻击，加密的轮次也只有6轮，今年ROUND提升到16后，直接排除一般的插值攻击

由题目分析知，给出pt的左半边均固定，所以输入形式为$(C, x),C\in GF(2^{24})$，查阅资料找到以下算法：

但实现以后发现计算$3^{15}+1$个(x, y)的拉格朗日插值多项式时间复杂度接近$O(2^{48})$

晚上又在上面的算法基础上，加了中间相遇的优化，将问题转化为n元1次方程组的求解，时间复杂度上可行，但$n\approx 40000$，内存消耗直接飙到2T，难顶

[赛后复现]

De1ta官方wp用的做法是高次积分攻击，原理分析起来也不难，但这里用的是rank1队伍用的另一种解法（借助$GF(2^{24})$上的单位根）

他们一开始用的也是中间相遇攻击，即用$g(x)$和$h(y,z)$作为purε正向和逆向的函数表示

对于第i轮的输出左侧，$deg_{x}(g)=3^{i-1}$，对于右侧，$deg_{x}(g)=3^{i}$；

逆向来看，对于左侧，$deg_{y}(h)=3^{16-m},deg_{z}(h)=3^{15-m}$，右侧，$deg_{y}(h)=3^{15-m},deg_{z}(h)=3^{14-m}$.

但如果直接中间相遇攻击求解多项式的系数，就会遇到先前我说的空间复杂度凉凉

所以他们丢弃了$h(y,z)$，改用$g(x)$和单位根进行求解，具体如下：

$GF(2^{24})^{*}$上，基于阶为$2^{24}-1$的事实，任意d次单位根$\omega$都可表示为$g^{\frac{2^{24}-1}{d}}$（g为$GF(2^{24})$上的生成元）

且$1+\omega+\omega^{2}+…+\omega^{d-1}=0$，易知$\sum_{i=0}^{d-1}\omega^{ij}=0$在$d\nmid j$时均成立，反之≠0（画个单位圆差不多就get了

所以随机取$a\in GF(2^{24})$，在$deg(g)<d$时，均有

$\sum^{d-1}_{i=0}g(a\omega^{i})=g(0)$

设第i轮后的密文为$(l_{i},r_{i})$，则第i-1轮后的密文为$(r_{i}+(l_{i}+k_{i})^{3},l_{i})=((r_{i}+l_{i}^{3})+l_{i}^{2}k_{i}+l_{i}k_{i}^{2}+k_{i}^{3},l_{i})$

可以看到第i-1轮左侧$k_{i}$的依赖项为$l_{i}^{2},l_{i}$，再基于前面提到的第i轮时，左侧$deg_{x}(g)=3^{i-1}$，如果$l_{i}$的$degree<d$，则$g(0)+\sum l_{i}=0$，且$k_{i}^{3}$的系数1一定累加偶数次（因为$d\mid (2^{24}-1)\Rightarrow 2\nmid d$），即累加后三次项的系数一定为0，这样就会导致所有$k_{i}$的依赖项等于0，求解失败

于是令$3^{i-1}>d,3^{i-2}<d,d\mid (2^{24}-1)$，比如求解k15时，取$d=\frac{2^{24}-1}{3}$，求解k14时，$d//=3$，问题转化为向量相加并求解二次方程根，时间复杂度控制在$O(2^{24})$下

求解出k14,k15后，根据题目中最后给出的

p = sympy.nextprime(2**24)
arr = np.random.randint(0,p,(ROUND,ROUND-2),dtype='int64')
keys = np.array(keys)
res = np.mod(np.dot(keys,arr),p)

问题即转化为

p = next_prime(2^24)
Fp = Zmod(p)
A = Matrix(Fp, 16, 14, arr[:16*14])
B = vector(Fp, arr[-14:])
K = A.delete_rows([14, 15]).solve_left(B - k14 * A[14] - k15 * A[15])

[exp]

1	from tqdm import tqdm

1
2
3

F.<a> = GF(2^24)
toF = F.fetch_int
fromF = lambda i : i.integer_representation()

# get data
data = dict()
for pt, ct in zip(open('pt.txt'), open('ct.txt')):
    pt = pt.rstrip('\n')
    ptr = toF(int(pt[6:], 16))
    ct = ct.rstrip('\n')
    ctl = toF(int(ct[:6], 16))
    ctr = toF(int(ct[6:], 16))
    data[ptr] = (ctl, ctr)

omega = F.gen()^3 # ((2^24-1)/3)th root of unity
poly = vector(F, 4) # polynomial for k_15
a = toF(2333) # ini
for i in tqdm(range((2**24-1)//3)):
    r, l = data[a] # swap
    v = vector(F, [l ^ 3 + r, l ^ 2, l, 1])
    poly += v
    a *= omega
r, l = data[toF(0)]
poly += vector(F, [l ^ 3 + r, l ^ 2, l, 1])

100%|██████████| 5592405/5592405 [04:04<00:00, 22915.12it/s]

R = PolynomialRing(F, names='k')
k = R.gen()
eq = poly[0] + poly[1] * k + poly[2] * k^2 + poly[3] * k^3
k15s = [r[0] for r in eq.roots()]
print([fromF(_) for _ in k15s])

[4122190, 14944194]

k1415 = []
for k15 in k15s:
    omega = F.gen()^9 # ((2^24-1)/9)th root of unity
    poly = vector(F, 4) # polynomial for k_14
    a = toF(2333) # ini
    for i in tqdm(range((2**24-1)//9)):
        r, l = data[a] # swap
        l, r = r + (l + k15) ^ 3, l
        v = vector(F, [l ^ 3 + r, l ^ 2, l, 1])
        poly += v
        a *= omega
    r, l = data[toF(0)]
    l, r = r + (l + k15) ^ 3, l
    poly += vector(F, [l ^ 3 + r, l ^ 2, l, 1])
    eq = poly[0] + poly[1] * k + poly[2] * k^2 + poly[3] * k^3
    k14s = [r[0] for r in eq.roots()]
    for k14 in k14s:
        k1415.append((fromF(k14), fromF(k15)))
        print((fromF(k14), fromF(k15)))

100%|██████████| 1864135/1864135 [01:27<00:00, 21343.81it/s]
  0%|          | 2069/1864135 [00:00<01:30, 20685.68it/s]

(2216205, 4122190)
(14035807, 4122190)


100%|██████████| 1864135/1864135 [01:26<00:00, 21605.20it/s]

(5546654, 14944194)
(9208218, 14944194)

1 2	import re arr = re.findall(r"\d+", open("data.txt", "r").read())

p = next_prime(2^24)
Fp = Zmod(p)
A = Matrix(Fp, 16, 14, arr[:16*14])
B = vector(Fp, arr[-14:])

Ks = []
for k14, k15 in k1415:
    K = A.delete_rows([14, 15]).solve_left(B - k14 * A[14] - k15 * A[15])
    Ks.append(K.list() + [k14, k15])

for k in Ks:
    l = toF(0x777777)
    r = toF(2333)
    for i in range(16):
        l , r = r , l + (r + toF(int(k[i]))) ^ 3
    l, r = r, l
    if (l, r) == data[toF(2333)]:
        key = k
        print(key)
        break

[16359893, 9091260, 11254674, 353718, 5395716, 9319892, 2360013, 12784246, 9857353, 2940944, 964650, 3296014, 7022345, 198188, 9208218, 14944194]

1	from Crypto.Util.number import *

cipher = 'd519b93b0fd950bdf1e1c321fc32e4c4c4b225b80c1ba091f31217b90132ed107e1f6b1c9dd60ba0eafcdd5923764c46'
flag = b''
for i in range(0, len(cipher), 12):
    r, l = toF(int(cipher[i:i+6], 16)), toF(int(cipher[i+6:i+12], 16))
    for j in range(16):
        l, r = r + (l + toF(int(key[15-j]))) ^ 3, l
    l, r = fromF(l), fromF(r)
    flag += (long_to_bytes(l) + long_to_bytes(r))
print(flag)

b'De1CTF{6a2ddcc3-c729-48f8-b5e0-7574c46a2846}\x04\x04\x04\x04'

[More]

比赛期间其实已经找到高次积分攻击相关的内容了- -但是他后面给了张表（15 ROUND要跑31h），直接劝退，看到官方wp的时候（一脸懵），然后再看了下表上的测试用cpu，奔腾4…👴佛辣