R1CS of zk-SNARKS
需提前将待证明的命题表达为 R1CS (Rank One Constraint System)
e.g. 给定等式$x_{1}^{2}x_{2}+x_{1}+1=22\ (x_{1}=3,x_{2}=2)$,将其化简如下(单元仅包含加/减/乘)
$y=x_{1}+1\quad\leftarrow(1)$
$z=x_{1}\cdot x_{1}\quad\leftarrow(2)$
$u=z\cdot x_{2}\quad\leftarrow(3)$
$v=u+y\quad\leftarrow(4)$
令解向量$s=(const,x_{1},x_{2},y,z,u,v)=(1,3,2,4,9,18,22)$
$\langle s,a\rangle\cdot\langle s,b\rangle=\langle s,c\rangle$
for (1), $a=(1,1,0,0,0,0,0),b=(1,0,0,0,0,0,0),c=(0,0,0,1,0,0,0)$
for (2), $a=(0,1,0,0,0,0,0),b=(0,1,0,0,0,0,0),c=(0,0,0,0,1,0,0)$
for (3), $a=(0,0,0,0,1,0,0),b=(0,0,1,0,0,0,0),c=(0,0,0,0,0,1,0)$
for (4), $a=(0,0,0,1,0,1,0),b=(1,0,0,0,0,0,0),c=(0,0,0,0,0,0,1)$
从上述向量扩展到矩阵$A,B,C$
$m=A\cdot s^{T},n=B\cdot s^{T},p=C\cdot s^{T}$
for i in range(4), $m_{i}\cdot n_{i}=p_{i}$.
对A,B,C矩阵作压缩 => 多项式向量$(A_1,A_2,A_3,A_4,A_5,A_6,A_7)$
即每列作拉格朗日插值,e.g.
Matrix A的col2 (1,1,0,0),视作多项式$A_2(x)$经过点(1,1),(2,1),(3,0),(4,0)
则$A_{2}(x)=1\cdot\frac{(x-2)(x-3)(x-4)}{(1-2)(1-3)(1-4)}+1\cdot\frac{(x-1)(x-3)(x-4)}{(2-1)(2-3)(2-4)}+0\cdot\frac{(x-1)(x-2)(x-4)}{(3-1)(3-2)(3-4)}+0\cdot\frac{(x-1)(x-2)(x-3)}{(4-1)(4-2)(4-3)}$
$s\cdot A(x)*s\cdot B(x)-s\cdot C(x)=H(x)Z(x)$, 其中$Z(x)=(x-1)(x-2)(x-3)(x-4)$
即表示x取1,2,3,4时,左式得到的多项式取值为0
zk-SNARKS
假设Alice已知$x_{1}^{2}x_{2}+x_{1}+1=22$的解,要向Bob证明其持有解,但不能直接公开解(零知识证明)
Bob随机选取点t,该抽样点的值不能让Alice获知,但需要Alice给出P(t), H(t),供Bob校验是否满足P(t)=H(t)Z(t)
利用加法同态隐藏抽样点
Bob不直接发送抽样点t的值,而是通过同态运算E(Alice无法复刻)
发送t的一系列指数映射$E(t^{0}),E(t^{1}),E(t^{2}),…$,Alice利用这些值计算E(P(t)),E(H(t))并供Bob验证
Bob计算Z(t)后映射至E(Z(t)),验证E(P(t)) ?= $E(E^{-1}(E(H(t)))Z(t))$
但仍存在问题,
Alice可以自生成A’(x),B’(x),C’(x),其s’满足s’A’(x)*s’B’(x)-s’C’(x)=H’(n)Z(n),则也能绕过验证
因此令,
则QAP转化为$A(x)B(x)-C(x)?=H(x)Z(x)$
Bob发送M个二元对,$(E(A_{1}(t)),E(\alpha_{a}A_{1}(t))),(E(A_{2}(t)),E(\alpha_{a}A_{2}(t))),…(E(A_{M}(t)),E(\alpha_{a}A_{M}(t)))$
(其中$\alpha_{a}$是Bob生成的随机数,M是多项式向量A(x)的维度)
由加法同态,有$E(\alpha_{a}A_{i}(t))=\alpha_{a}E(A_{i}(t))$
Alice通过计算$\sum s_{i}E(A_{i}(t))$得到$E(A(t))$,并类似得到$E(\alpha_{a}A(t))$
类似的要求Alice计算出对应B和C的二元对后,仍存在问题,即无法确定Alice用于约束$A_{i}(t),B_{i}(t),C_{i}(t)$所用的s向量相同
因此引入多项式序列L(x),其中$L_{i}(x)=A_{i}(x)+B_{i}(x)+C_{i}(x)$
选取随机数$\beta$,Bob发送M个二元对,
$(E(L_{1}(t)),E(\beta L_{1}(t))),(E(L_{2}(t)),E(\beta L_{2}(t))),…,(E(L_{M}(t)),E(\beta L_{M}(t)))$
Alice计算$E(L(t))=\sum s_{i}E(L_{i}(t)),E(\beta L(t))=\sum s_{i}E(\beta L_{i}(t))$
校验$E(\beta L(t))?=\beta(E(A(t))+E(B(t))+E(C(t)))$,(因为只有当约束A,B,C,L的所用向量相同时才成立)
最后发送$E(t^{0}),E(t^{1}),E(t^{2}),…$,供Alice计算E(H(t))
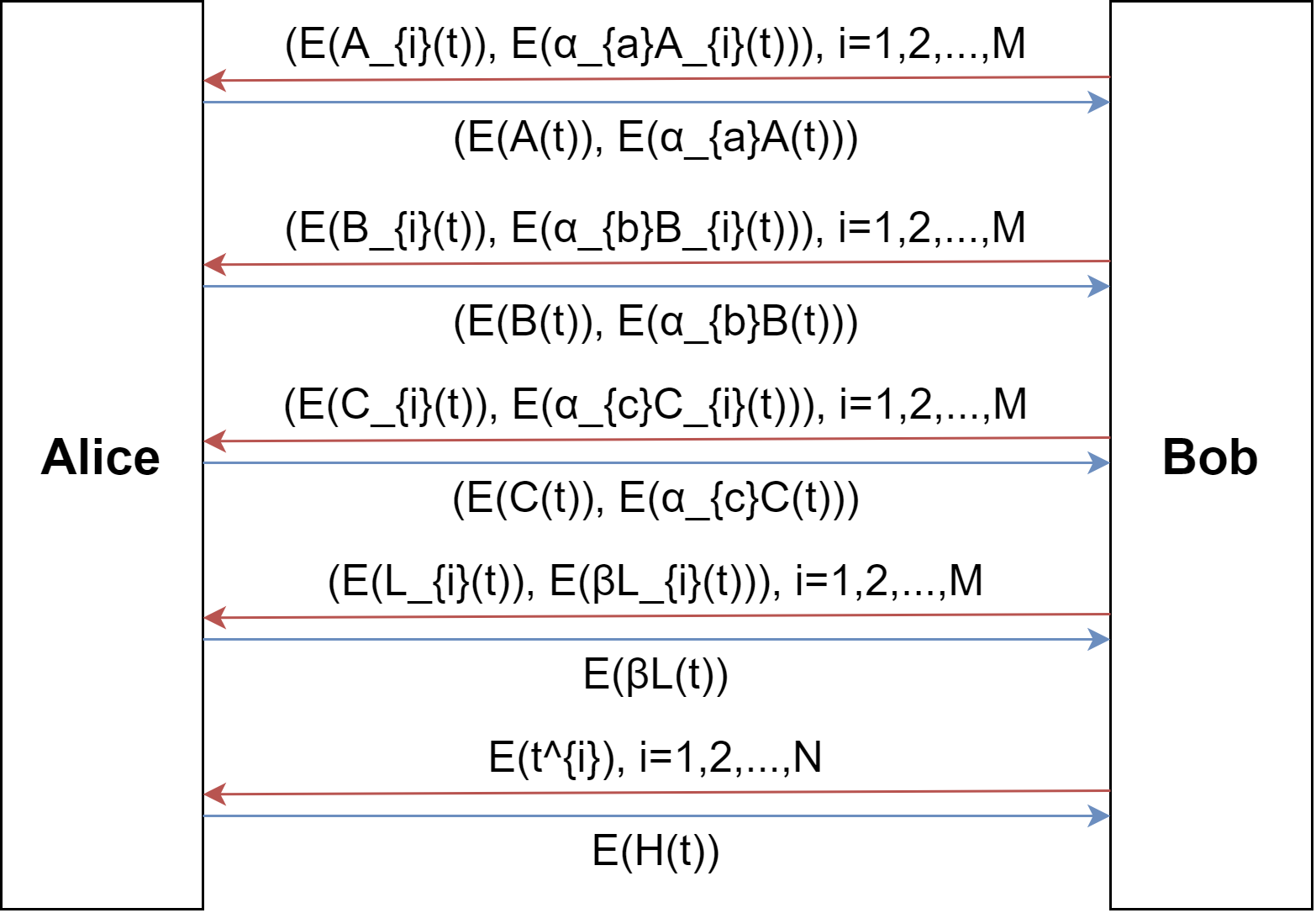
1) $E(\alpha_{a}A(t))?=\alpha_{a}E(A(t))$校验Alice传回的E(A(t))是否为$E(A_{i}(t))$的线性组合,B,C类似
2) $E(\beta L(t))?=\beta(E(A(t))+E(B(t))+E(C(t)))$校验A,B,C中使用的为同一个解向量s
3) $E(A(t)B(t)-C(t))?=E(H(t)Z(t))$校验使用的解向量s是否正确
实际方案
上述所使用的同态加法运算E在椭圆曲线上,因此无法实现高效的$E^{-1}$,考虑引入双线性对
$G_1,G_2,G_T$为n阶乘法循环群(椭圆曲线上加法),一个双线性对e就是一个从$G_1\times G_2$到$G_T$的双线性映射
其中满足的最重要一条性质即为双线性性:
$g_1\in G_1,g_2\in G_2,e(g_1^a,g_2^b)=e(g_1,g_2)^{ab}$.
(椭圆曲线) 假设$G_1$上的加法同态运算定义为$E_1$(基点*x), $G_2$上的加法同态定义作$E_2$,则
$e(E_1(x),E_2(y))=e(E_1(u),E_2(v)),xy=uv$.
通过双线性对,当t = xy = uv时,
$E(t)=e(E_1(x),E_2(y))=e(E_1(u),E_2(v))$
且$E(ax+by)=e(E_1(ax+by),E_2(1))=e(aE_1(x)+bE_1(y),E_2(1))=aE(x)+bE(y)$,满足加法同态
因此可采用共同参考数据集(CRS)实现以下zk-SHARKS流程:
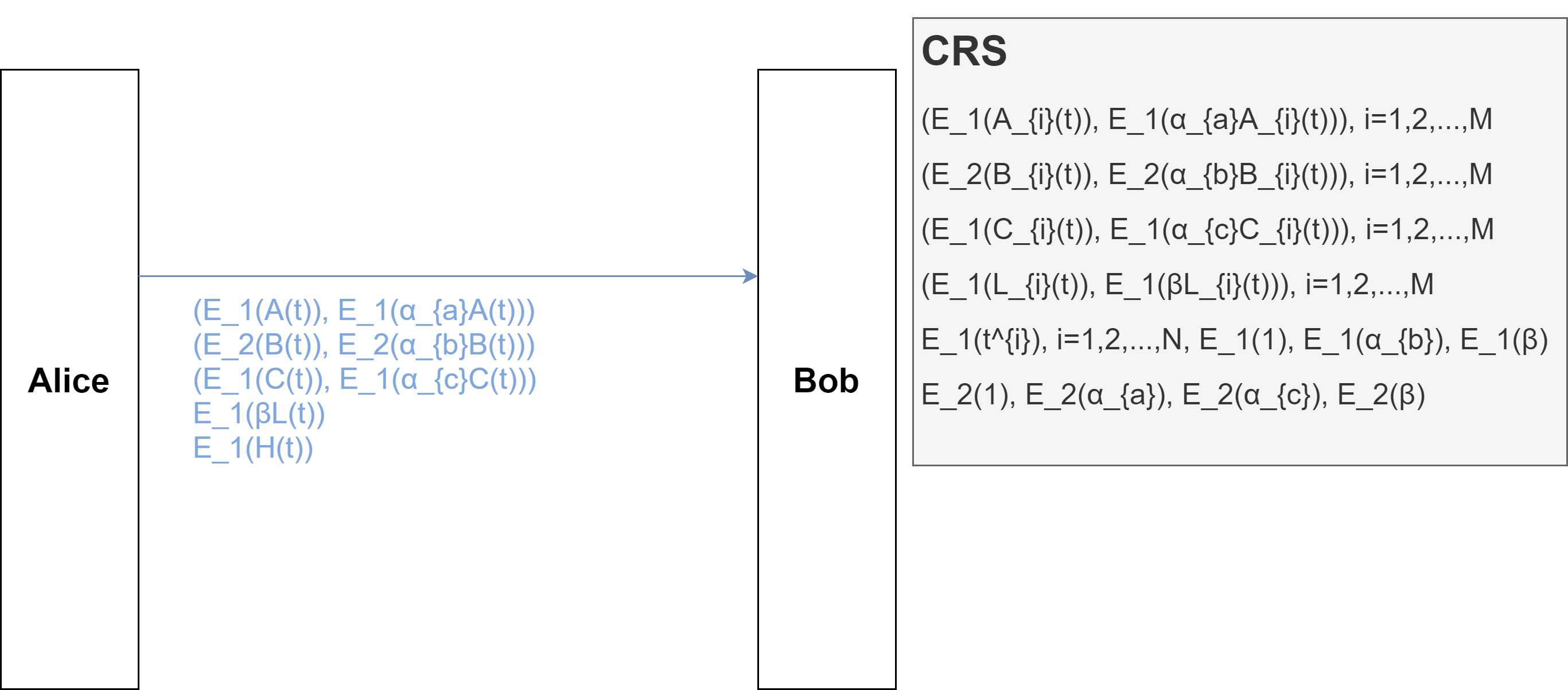
1) $e(E_1(A(t)),E_2(\alpha_{a}))?=e(E_1(\alpha_{a}A(t)),E_2(1))$,校验Alice传回的$E_1(A(t))$是否为$E_1(A_{i}(t))$的线性组合
2) $e(E_1(\alpha_{b}),E_2(B(t)))?=e(E_1(1),E_2(\alpha_{b}B(t)))$,校验Alice传回的$E_2(B(t))$是否为$E_2(B_{i}(t))$的线性组合
3) $e(E_1(C(t)),E_2(\alpha_{c}))?=e(E_1(\alpha_{c}C(t)),E_2(1))$,校验Alice传回的$E_1(C(t))$是否为$E_1(C_{i}(t))$的线性组合
4) $e(E_1(βL(t)),E_2(1))?=E(\beta(A(t)+B(t)+C(t)))=e(E_1(A(t))+E_1(C(t)),E_2(\beta))+e(E_1(\beta),E_2(B(t)))$,校验A,B,C中使用的为同一个解向量s
5) $e(E_1(A(t)),E_2(B(t)))?=e(E_1(H(t)),E_2(Z(t)))+e(E_1(C(t)),E_2(1))$,校验向量s正确性
zcash构建zk-SNARKS
https://m.mytokencap.com/news/116994
利用 libsnark 库开发 zk-SNARKs