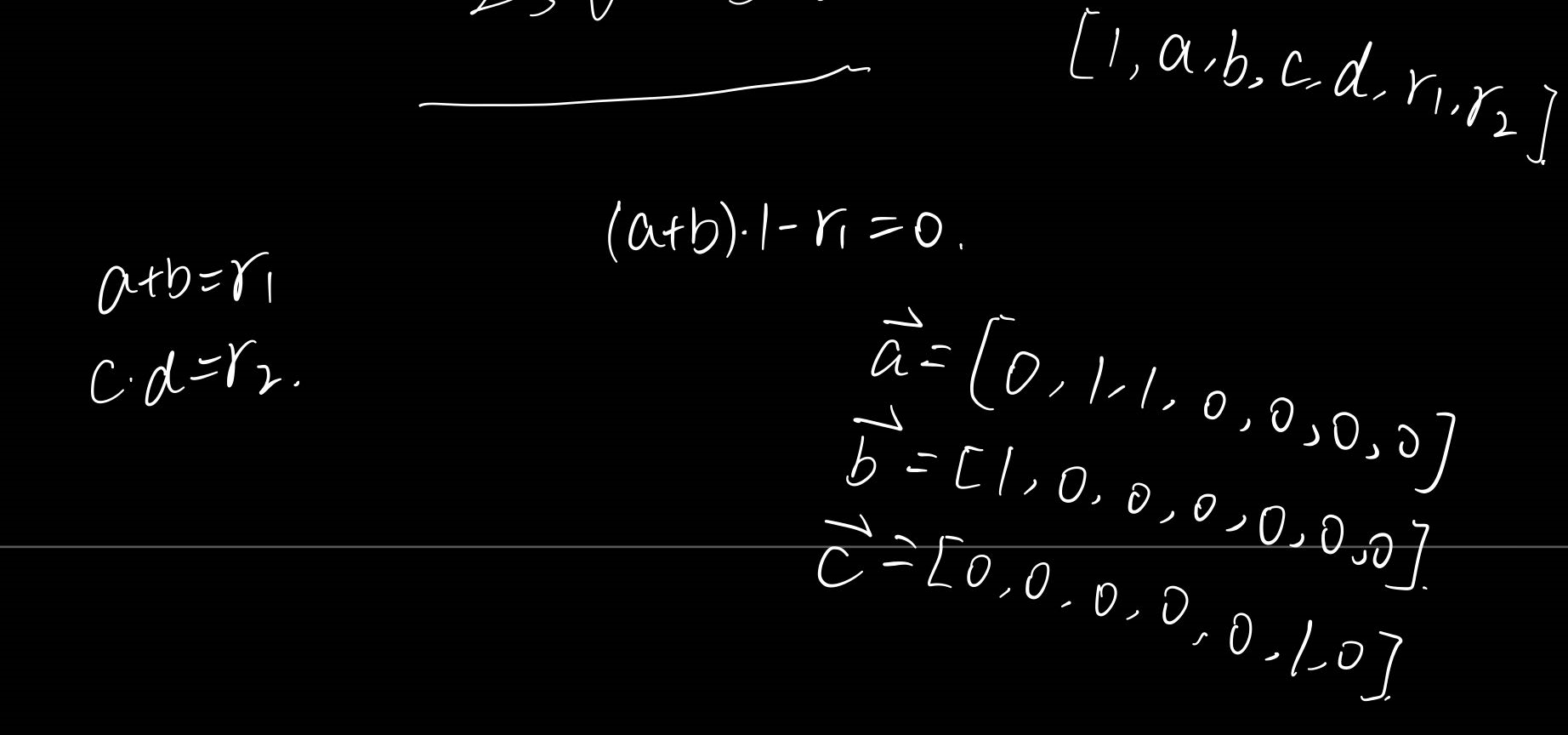Compile circom and test

circom+snarkjs测试（e.g. bn.circom）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
circom bn.circom --r1cs --wasm --sym --c
cd bn_js
# create input.json in bn_js

snarkjs wc bn.wasm input.json witness.wtns

snarkjs powersoftau new bn128 12 pot12_0000.ptau -v
snarkjs powersoftau contribute pot12_0000.ptau pot12_0001.ptau --name="First contribution" -v

snarkjs powersoftau prepare phase2 pot12_0001.ptau pot12_final.ptau -v
snarkjs g16s ../bn.r1cs pot12_final.ptau bn_0000.zkey
snarkjs zkey contribute bn_0000.zkey bn_0001.zkey --name="1st Contributor Name" -v

snarkjs zkey export verificationkey bn_0001.zkey verification_key.json

snarkjs g16p bn_0001.zkey witness.wtns proof.json public.json
snarkjs g16v verification_key.json public.json proof.json

https://github.com/iden3/snarkjs

Scalar size does not match

circom (groth16) 不允许输出门只有add operation的情况，当constraints: 0时，生成proof会报错：

1
[ERROR] snarkJS: Error: Scalar size does not match

image-20230521204450656

但有multiply operation时，circom编译会做处理，使得约束整合成quadratic的形式（\(A*B-C=0\)），并压缩电路大小：

image-20230521142208277 
1
2
3
4
c <== a + b;
d <== a * b;

[-a] * [c - a] - [-d] = 0

[TODO] 但对于以下约束：

1
2
r1 <== a + b;
r2 <== c * d;

snarkjs rp打印出来的r1cs约束直接不包含r1 <== a + b，

image-20230523173213698

但实际上加法约束也能拍平成R1CS，因此该问题（吞约束）待解决：

image-20230523172955578

Non quadratic constraints are not allowed

circom无法直接处理%，>>，**等约束，会报错Non quadratic constraints are not allowed

test_mod.circom

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// without LessThan, constraints: 0, [ERROR] snarkJS: Error: Scalar size does not match
template test_mod(wbits, b) {
    assert(wbits <= 252);
    signal input a;
    signal output r;    // a = q * b + r

    // signal q;
    // q <-- a \ b;
    r <-- a % b;

    component lessThan = LessThan(wbits);
    lessThan.in[0] <== r;
    lessThan.in[1] <== b;
    lessThan.out === 1;

    // a === q * b + r;
}
image-20230522095150094

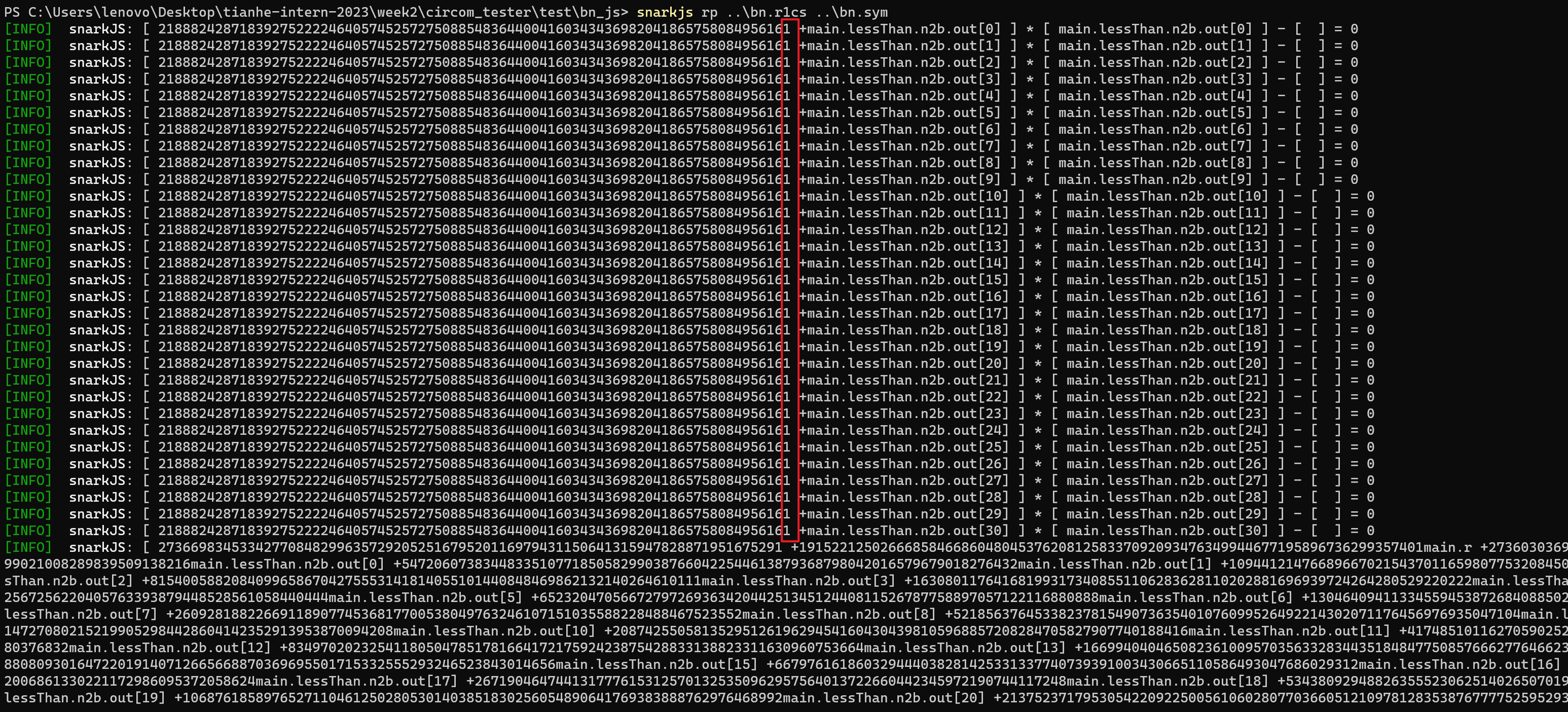
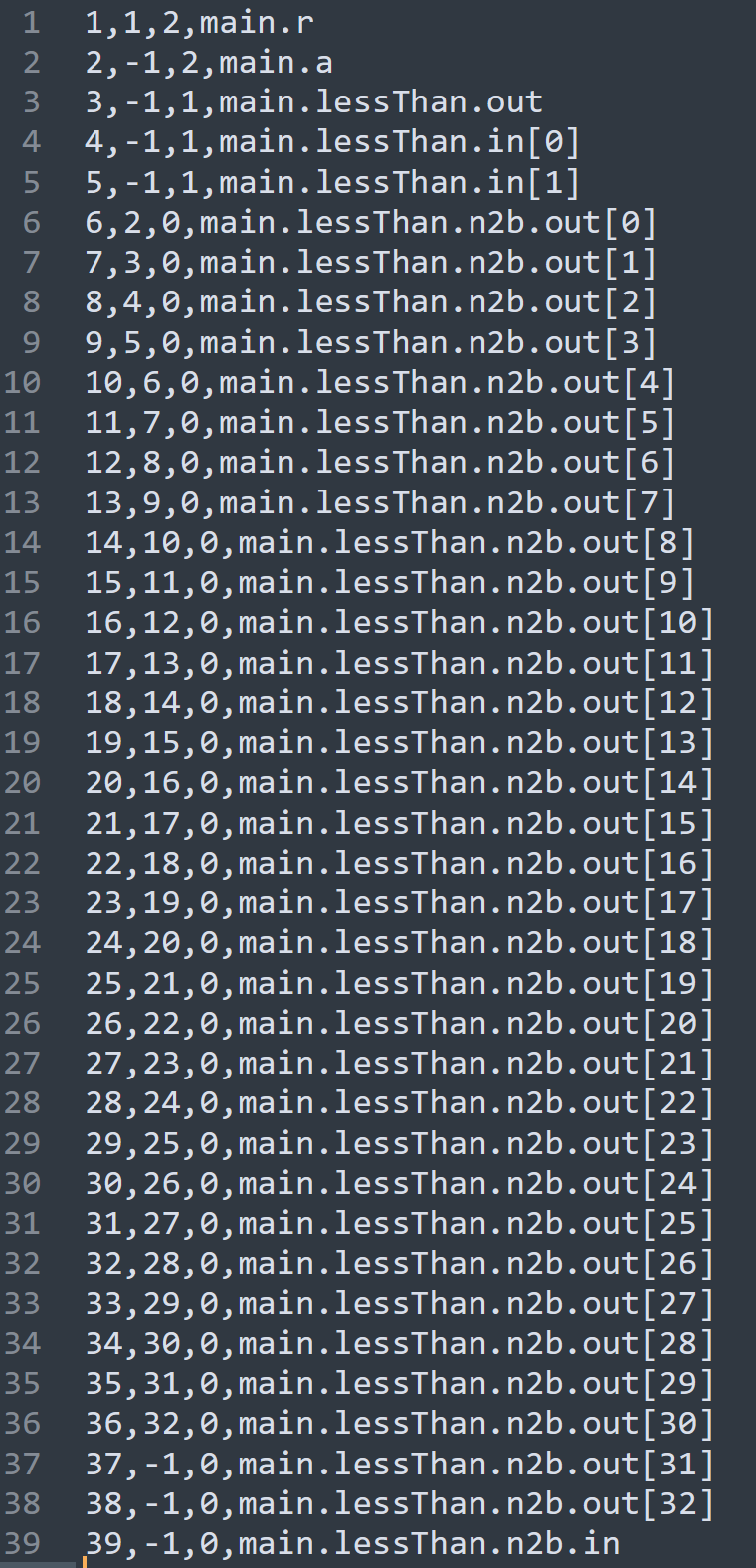
需要注意的是，snarkjs rp打印出的R1CS约束，在常数项的x*1并不显示*，因此实际上前若干项[ 218882428718392752222464057452572750885483644004160343436982041865758084956161 +main.lessThan.n2b.out[i] ] * [ main.lessThan.n2b.out[i] ] - [ ] = 0表示约束[ -1 +main.lessThan.n2b.out[i] ] * [ main.lessThan.n2b.out[i] ] - [ ] = 0

image-20230522095332316

在对应的bn.sym符号表中，可以看到circom简化了约束（移除部分signal）

test_rsh.circom

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template test_rsh(wbits, b) {
    assert(wbits <= 253);
    signal input a;
    signal output r;

    signal check_a;
    component lessThan = LessThan(wbits);

    r <-- a >> b;
    check_a <== r * (1 << b);

    lessThan.in[0] <== a - check_a;
    lessThan.in[1] <== (1 << b); 
    lessThan.out === 1;
}

test_dlp.circom

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template test_dlp(a, n) {
    signal input x; // n-bit
    signal output y;    // y = a ^ x

    component n2b = Num2Bits(n);
    n2b.in <== a;

    signal y1[n];
    signal y2[n - 1];
    y1[0] <== 1;
    for (var i = 1; i < n; i++) {
        var tmp = n2b.out[n - i] * (a - 1) + 1;
        y2[i - 1] <== tmp * y1[i - 1];
        y1[i] <== y2[i - 1] * y2[i - 1];
    }
    var tmp = n2b.out[0] * (a - 1) + 1;
    y <== y1[n - 1] * tmp;
}

dlp的思路是调用Num2Bits，再基于快速幂（在每一位上做条件乘法和平方）

进一步，若r = rsh(a>>b)的b也作为witness，则可以通过dlp组件获得c = 2 ^ b，再创建约束check_a <== c * r，最后调用LessThan组件即可