Assignment

略

Record

实现DES的时候发现性能一直提不上去（v1测试后≈750us/KB，距离要求的500Mbps还有亿点点距离…🤦‍）

在此记录尝试提升性能过程中更迭的几个版本

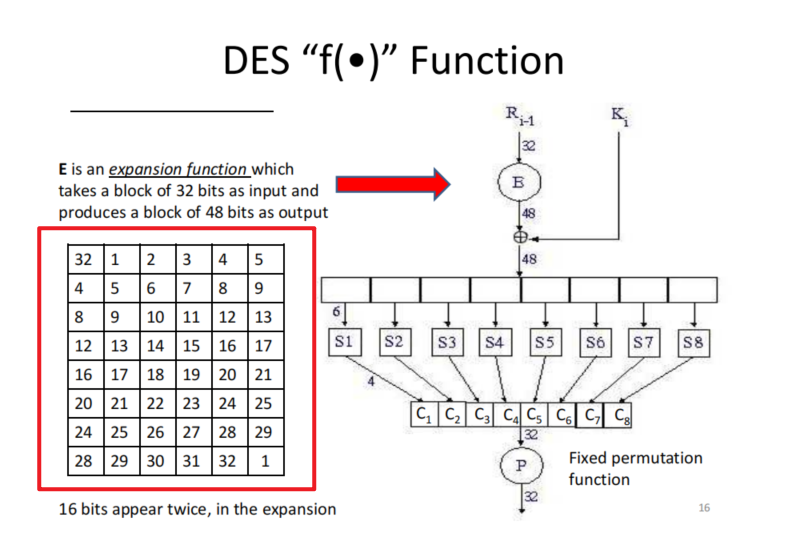
Combine S and P boxes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
static uint32_t spbox[8][64];

void gen_spbox() {
    for (int i = 0; i < 8; i++) {
        for (int j = 0; j < 64; j++) {
            spbox[i][j] = 0;
            int real_j = ((((j >> 4) & 0x02) | (j & 0x01)) << 4) | ((j >> 1) & 0x0f);
            for (int k = 0; k < 4; k++) {
                if (sbox[i][real_j] & (0x08 >> k)) {
                    spbox[i][j] |= 1 << (32 - inv_pbox[4 * i + k]);
                }
            }
//#ifdef DEBUG
//            printf("spbox[%d][%2d]=%08x\n", i, j, spbox[i][j]);
//#endif
        }
    }
}
Construct fewer Bit Operations

开销主要在于BIT_TO_BYTE和BYTE_TO_BIT 👉 IP，PC-1，PC-2等置换均是基于bit数组上做的处理

因此参考mbed TLS，摒弃bit数组，构造更少步骤的位运算来提升性能

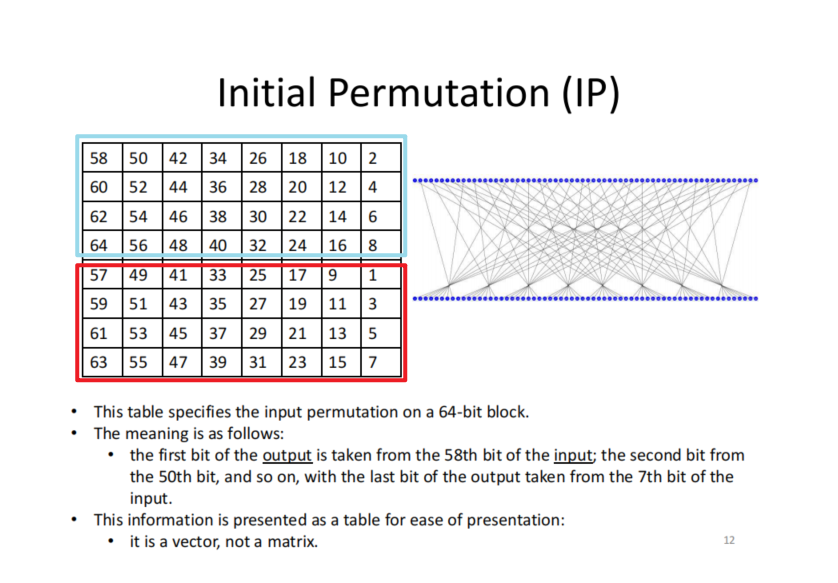
  • Initial Permutation (IP)

    mbed TLS用到一个小trick：

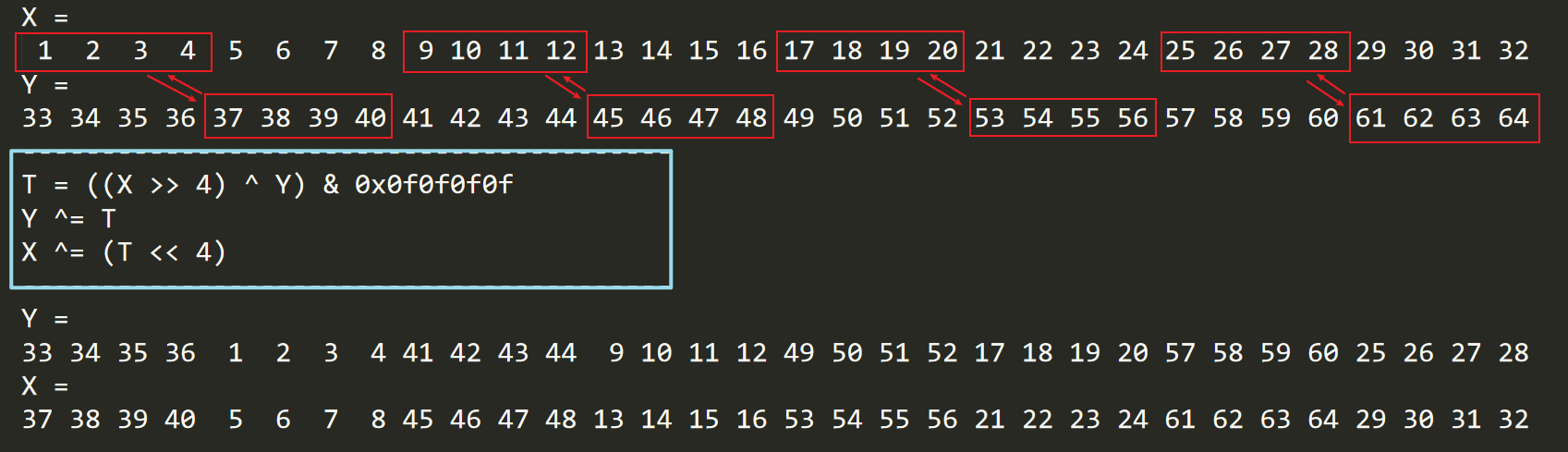
    可以达到类似shuffle的目的，我们再回过头来看IP：

    逆推回初始的X = [1 2 … 32], Y = [33 34 … 64]状态（找如何shuffle能得到连续序列）

    逆推过程的逻辑很清晰，但不在此特意画出，下面是正向的变换逻辑：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    X = 
     1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
    Y = 
    33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
    -----------------------------------------
    T = ((X >> 4) ^ Y) & 0x0f0f0f0f
    Y ^= T  
    X ^= (T << 4)
    -----------------------------------------
    Y = 
    33 34 35 36  1  2  3  4 41 42 43 44  9 10 11 12 49 50 51 52 17 18 19 20 57 58 59 60 25 26 27 28
    X = 
    37 38 39 40  5  6  7  8 45 46 47 48 13 14 15 16 53 54 55 56 21 22 23 24 61 62 63 64 29 30 31 32
    -----------------------------------------
    T = ((X >> 16) ^ Y) & 0x0000ffff
    Y ^= T
    X ^= (T << 16)
    -----------------------------------------
    Y = 
    33 34 35 36  1  2  3  4 41 42 43 44  9 10 11 12 37 38 39 40  5  6  7  8 45 46 47 48 13 14 15 16
    X = 
    49 50 51 52 17 18 19 20 57 58 59 60 25 26 27 28 53 54 55 56 21 22 23 24 61 62 63 64 29 30 31 32
    -----------------------------------------
    T = ((Y >> 2) ^ X) & 0x33333333
    X ^= T
    Y ^= (T << 2)
    -----------------------------------------
    X = 
    49 50 33 34 17 18  1  2 57 58 41 42 25 26  9 10 53 54 37 38 21 22  5  6 61 62 45 46 29 30 13 14
    Y = 
    51 52 35 36 19 20  3  4 59 60 43 44 27 28 11 12 55 56 39 40 23 24  7  8 63 64 47 48 31 32 15 16
    -----------------------------------------
    T = ((Y >> 8) ^ X) & 0x00ff00ff
    X ^= T
    Y ^= (T << 8)
    -----------------------------------------
    X = 
    49 50 33 34 17 18  1  2 51 52 35 36 19 20  3  4 53 54 37 38 21 22  5  6 55 56 39 40 23 24  7  8
    Y = 
    57 58 41 42 25 26  9 10 59 60 43 44 27 28 11 12 61 62 45 46 29 30 13 14 63 64 47 48 31 32 15 16
    -----------------------------------------
    Y = ((Y << 1) & 0xffffffff) | (Y >> 31)
    -----------------------------------------
    X = 
    49 50 33 34 17 18  1  2 51 52 35 36 19 20  3  4 53 54 37 38 21 22  5  6 55 56 39 40 23 24  7  8
    Y = 
    58 41 42 25 26  9 10 59 60 43 44 27 28 11 12 61 62 45 46 29 30 13 14 63 64 47 48 31 32 15 16 57
    -----------------------------------------
    T = (X ^ Y) & 0xaaaaaaaa
    X ^= T
    Y ^= T
    -----------------------------------------
    X = 
    58 50 42 34 26 18 10  2 60 52 44 36 28 20 12  4 62 54 46 38 30 22 14  6 64 56 48 40 32 24 16  8
    Y = 
    49 41 33 25 17  9  1 59 51 43 35 27 19 11  3 61 53 45 37 29 21 13  5 63 55 47 39 31 23 15  7 57
    -----------------------------------------
    Y = ((Y << 31) & 0xffffffff) | (Y >> 1)
    -----------------------------------------
    X = 
    58 50 42 34 26 18 10  2 60 52 44 36 28 20 12  4 62 54 46 38 30 22 14  6 64 56 48 40 32 24 16  8
    Y = 
    57 49 41 33 25 17  9  1 59 51 43 35 27 19 11  3 61 53 45 37 29 21 13  5 63 55 47 39 31 23 15  7

  • PC-1

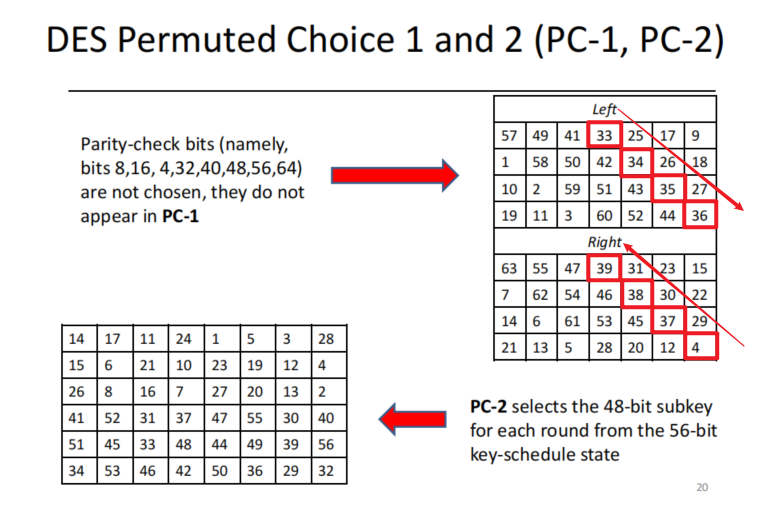
    注意到PC-1存在如图所示 步长为8 容量为4的连续序列，e.g. Left可将{33, 34, 35, 36}作为基准，打表

    1
    2
    3
    4
    5
    6
    static const uint32_t PC1_L[16] = {
            0x00000000, 0x00000001, 0x00000100, 0x00000101,
            0x00010000, 0x00010001, 0x00010100, 0x00010101,
            0x01000000, 0x01000001, 0x01000100, 0x01000101,
            0x01010000, 0x01010001, 0x01010100, 0x01010101
    };

    输入容量4的连续序列（共$2^4$种状态），将其填入PC-1后{33, 34, 35, 36}所在的位置（其他位置置零），此时输出的uint32_t即为数组上对应位置的值（输出值再整体左移/右移即可实现PC-1）

    Right则是以{39, 38, 37, 4}为基准，不同的是需要逆序输入

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    /*
     * based on {39, 38, 37, 4}
     * but input in `reverse` order
     */
    static const uint32_t PC1_R[16] = {
            0x00000000, 0x01000000, 0x00010000, 0x01010000,
            0x00000100, 0x01000100, 0x00010100, 0x01010100,
            0x00000001, 0x01000001, 0x00010001, 0x01010001,
            0x00000101, 0x01000101, 0x00010101, 0x01010101
    };

    但在此之前需要经过下述两次shuffle（同样也是通过PC-1后的状态来逆推）：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    X = 
     1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
    Y = 
    33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
    -----------------------------------------
    T = ((Y >> 4) ^ X) & 0x0f0f0f0f
    X ^= T
    Y ^= (T << 4)
    -----------------------------------------
    X = 
     1  2  3  4 33 34 35 36  9 10 11 12 41 42 43 44 17 18 19 20 49 50 51 52 25 26 27 28 57 58 59 60
    Y = 
     5  6  7  8 37 38 39 40 13 14 15 16 45 46 47 48 21 22 23 24 53 54 55 56 29 30 31 32 61 62 63 64
    -----------------------------------------
    T = (Y ^ X) & 0x10101010
    X ^= T
    Y ^= T
    -----------------------------------------
    X = 
     1  2  3  8 33 34 35 36  9 10 11 16 41 42 43 44 17 18 19 24 49 50 51 52 25 26 27 32 57 58 59 60
    Y = 
     5  6  7  4 37 38 39 40 13 14 15 12 45 46 47 48 21 22 23 20 53 54 55 56 29 30 31 28 61 62 63 64

    完整的PC-1相关代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    #define PC1(X, Y) {                                                             \
        uint32_t T;                                                                 \
        T = (((Y) >> 4) ^ (X)) & 0x0f0f0f0f; (X) ^= T; (Y) ^= (T << 4);             \
        T = ((Y) ^ (X)) & 0x10101010; (X) ^= T; (Y) ^= T;                           \
        (X) = (PC1_L[((X) >> 29) & 0x0f] << 4) | (PC1_L[((X) >> 24) & 0x0f])        \
          | (PC1_L[((X) >> 21) & 0x0f] << 5) | (PC1_L[((X) >> 16) & 0x0f] << 1)     \
          | (PC1_L[((X) >> 13) & 0x0f] << 6) | (PC1_L[((X) >>  8) & 0x0f] << 2)     \
          | (PC1_L[((X) >>  5) & 0x0f] << 7) | (PC1_L[(X      ) & 0x0f] << 3);      \
        (Y) = (PC1_R[((Y) >> 29) & 0x0f] >> 4) | (PC1_R[((Y) >> 25) & 0x0f])        \
          | (PC1_R[((Y) >> 21) & 0x0f] >> 3) | (PC1_R[((Y) >> 17) & 0x0f] << 1)     \
          | (PC1_R[((Y) >> 13) & 0x0f] >> 2) | (PC1_R[((Y) >>  9) & 0x0f] << 2)     \
          | (PC1_R[((Y) >>  5) & 0x0f] >> 1) | (PC1_R[((Y) >>  1) & 0x0f] << 3);    \
        (X) &= 0x0fffffff;                                                          \
        (Y) &= 0x0fffffff;                                                          \
    }

  • PC-2

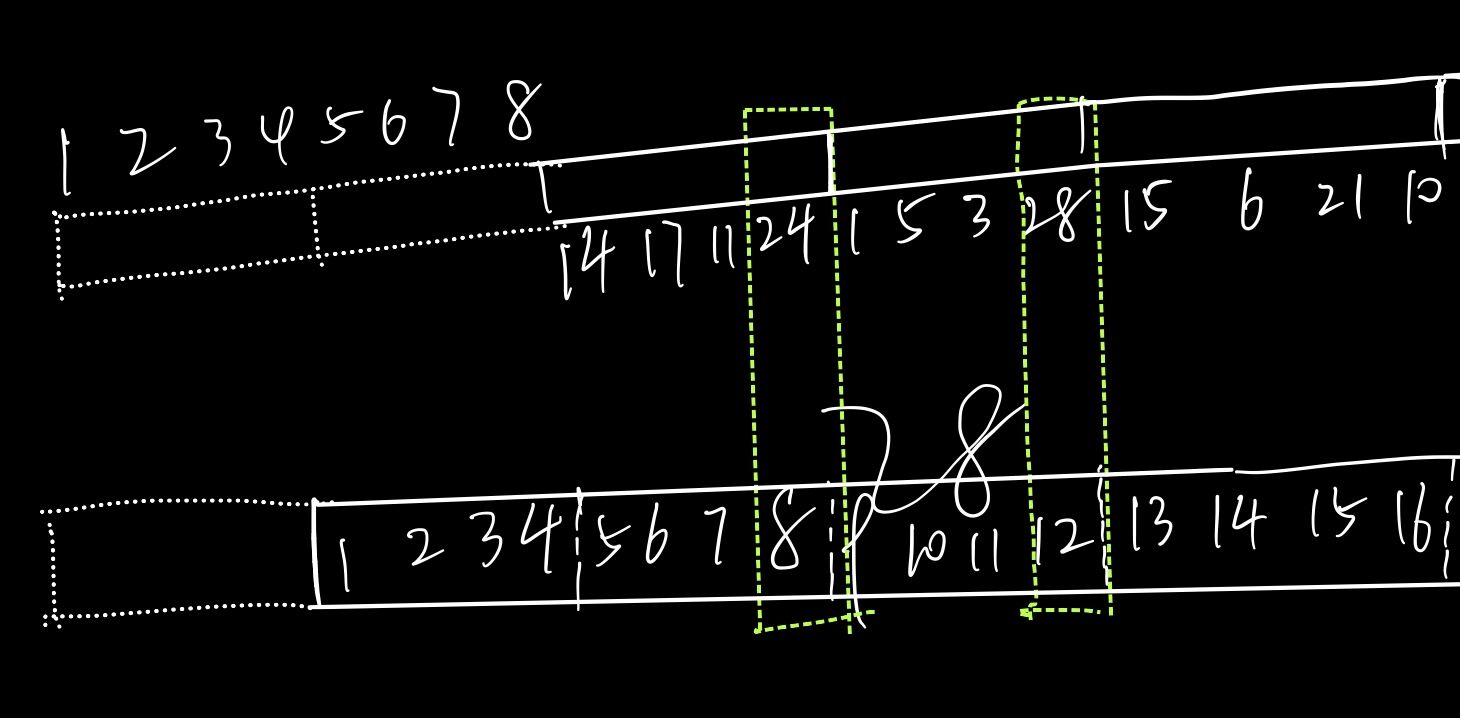
    PC-2就不存在和PC-1这样显著的特征，因此只能去将保持原有相对位置的bit划分至同一批处理，尽可能减少位运算步骤，e.g. 下图所示的原始第8、第12 bit能一起处理(((X) << 16) & 0x00110000)

    完整的PC-2相关代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    #define PC2(X, Y, K) {                                                  \
        (K)[0] = (((X) <<  9) & 0x00800000) | (((X) << 11) & 0x00400000)    \
             | (((X) <<  4) & 0x00200000) | (((X) << 16) & 0x00110000)      \
             | (((X) >>  8) & 0x000a4000) | (((X) >>  5) & 0x00040000)      \
             | (((X) <<  2) & 0x00008008) | (((X) <<  6) & 0x00002800)      \
             | (((X) <<  1) & 0x00000400) | (((X) >>  6) & 0x00001004)      \
             | (((X) >>  7) & 0x00000220) | (((X) >> 16) & 0x00000100)      \
             | (((X) <<  5) & 0x00000080) | (((X) >> 14) & 0x00000042)      \
             | (((X) >> 17) & 0x00000010) | (((X) >> 26) & 0x00000001);     \
        (K)[1] = (((Y) <<  8) & 0x00800100) | (((Y) << 18) & 0x00400000)    \
             | (((Y) >>  4) & 0x00200000) | (((Y) <<  1) & 0x00100000)      \
             | (((Y) << 10) & 0x00088000) | (((Y) << 17) & 0x00040000)      \
             | (((Y) >>  9) & 0x00020000) | ((Y      ) & 0x00010000)        \
             | (((Y) <<  3) & 0x00004440) | (((Y) >> 10) & 0x00002010)      \
             | (((Y) <<  4) & 0x00001000) | (((Y) >>  1) & 0x00000800)      \
             | (((Y) >>  8) & 0x00000200) | (((Y) >> 15) & 0x00000080)      \
             | (((Y) >>  5) & 0x00000020) | (((Y) >>  3) & 0x00000008)      \
             | (((Y) >> 18) & 0x00000004) | (((Y) >> 26) & 0x00000002)      \
             | (((Y) >> 24) & 0x00000001);                                  \
    }

  • Expansion Function

    image-20211028220127659

    每行均为连续序列，类似PC-2进行位处理（首末行特殊处理）

    轮函数代码实现如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    #define f(L, R, K) {                                                                        \
        (L) ^= spbox[0][((((R) >> 27) & 0x1f) | (((R) << 5) & 0x20)) ^ (((K)[0] >> 18) & 0x3f)] \
           | spbox[1][(((R) >> 23) & 0x3f) ^ (((K)[0] >> 12) & 0x3f)]                           \
           | spbox[2][(((R) >> 19) & 0x3f) ^ (((K)[0] >> 6) & 0x3f)]                            \
           | spbox[3][(((R) >> 15) & 0x3f) ^ (((K)[0]) & 0x3f)]                                 \
           | spbox[4][(((R) >> 11) & 0x3f) ^ (((K)[1] >> 18) & 0x3f)]                           \
           | spbox[5][(((R) >> 7) & 0x3f) ^ (((K)[1] >> 12) & 0x3f)]                            \
           | spbox[6][(((R) >> 3) & 0x3f) ^ (((K)[1] >> 6) & 0x3f)]                             \
           | spbox[7][((((R) << 1) & 0x3e) | (((R) >> 31) & 0x01)) ^ (((K)[1]) & 0x3f)];        \
    }

最后的性能测试在25us/KB左右👏算是一个比较显著的提升（

AES和SM4的相关性能优化trick实际上和前面在DES中gen_spbox()的预处理类似，本质上都是空间换时间（T表），不在此赘述

Reference

简化位运算相关可以移步这本书👇

https://books.google.com.hk/books?id=iBNKMspIlqEC&lpg=SL20-PA11&vq=Transposing+an+8x8-bit+matrix&pg=SL20-PA11&redir_esc=y#v=snippet&q=Transposing%20an%208x8-bit%20matrix&f=false