Bullet Proofs

Pedersen Commitment

$Com(v)=v\cdot B+\tilde{v}\cdot\tilde{B}$，其中$B,\tilde{B}$为椭圆曲线上的两个基点，$v$是需要承诺的秘密数，$\tilde{v}$为（随机）盲化因子。

具备同态加法特性，即：

$Com(v_1)+Com(v_2)=v_1\cdot B+\tilde{v_1}\cdot\tilde{B}+v_2\cdot B+\tilde{v_2}\cdot\tilde{B}=(v_1+v_2)\cdot B+(\tilde{v_1}+\tilde{v_2})\cdot\tilde{B}=Com(v_1+v_2)$

同态保证了UTXO交易中的Input/Output总和均是Pedersen Commitment

⭐(Pedersen Vector Commitment)

$\textbf{B}=(B_1,…,B_n)\in\mathbb{G}^n$

$Com(\textbf{v}=(v_1,…,v_n);\tilde{v})=\langle\textbf{v},\textbf{B}\rangle+\tilde{v}\tilde{B}$

Bullet Proofs

Notation

小写字母$a,b,c$表示$\mathbb{Z}_p$下的标量，大写字母$G,H,P,Q$表示群$\mathbb{G}$下的元素。向量被粗体表示，例如$\textbf{a},\textbf{G}$。

用到的Pedersen Vector Commitment定义为：

$$Com(\textbf{a}_L,\textbf{a}_R)=\langle\textbf{a}_L,\textbf{G}\rangle+\langle\textbf{a}_R,\textbf{H}\rangle+\tilde{a}\tilde{B}$$

其中$\textbf{G},\textbf{H}\in\mathbb{G}^n$

Inner-Product Range Proof

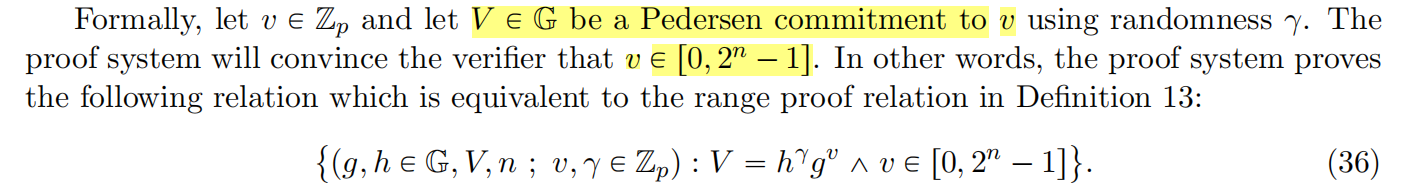
并将原论文中的乘法群以加法群代替，如下：

$\{(B,\tilde{B}\in\mathbb{G},V,n\ ;\ v,\tilde{v}\in\mathbb{Z}_p):V=vB+\tilde{v}\tilde{B}\ \wedge\ v\in[0,2^n-1]\}$

令$\textbf{a}_L=(a_1,…,a_n)\in\{0,1\}^n$表示由$v$各个比特位组成的向量，即$\langle\textbf{a}_L,\textbf{2}^n\rangle=v$ ← ①

还需要保证$\textbf{a}_L$仅包含$\{0,1\}$，因此令$\textbf{a}_R=\textbf{a}_L-\textbf{1}^n$ ← ②，有$\textbf{a}_L\circ\textbf{a}_R=\textbf{0}^n$ ← ③

做以下整理：

$$\langle\textbf{a}_L,\textbf{2}^n\rangle=v\ \wedge\langle\textbf{a}_L-\textbf{1}-\textbf{a}_R,\textbf{y}^n\rangle=0\ \wedge\ \langle\textbf{a}_L,\textbf{a}_R\circ\textbf{y}^n\rangle=0$$

可进一步，令verifier选取随机$z\in\mathbb{Z}_p$，将上述转为一个约束：

$$z^2\cdot v=z^2\langle\textbf{a}_L,\textbf{2}^n\rangle+z\langle\textbf{a}_L-\textbf{1}-\textbf{a}_R,\textbf{y}^n\rangle+\langle\textbf{a}_L,\textbf{a}_R\circ\textbf{y}^n\rangle$$

将其转化为前面论文中提到的”a single inner-product constraint”（并令$\textbf{a}_L$只出现在左侧，$\textbf{a}_R$只出现在右侧，不含witness的项合并即为$\delta$）：

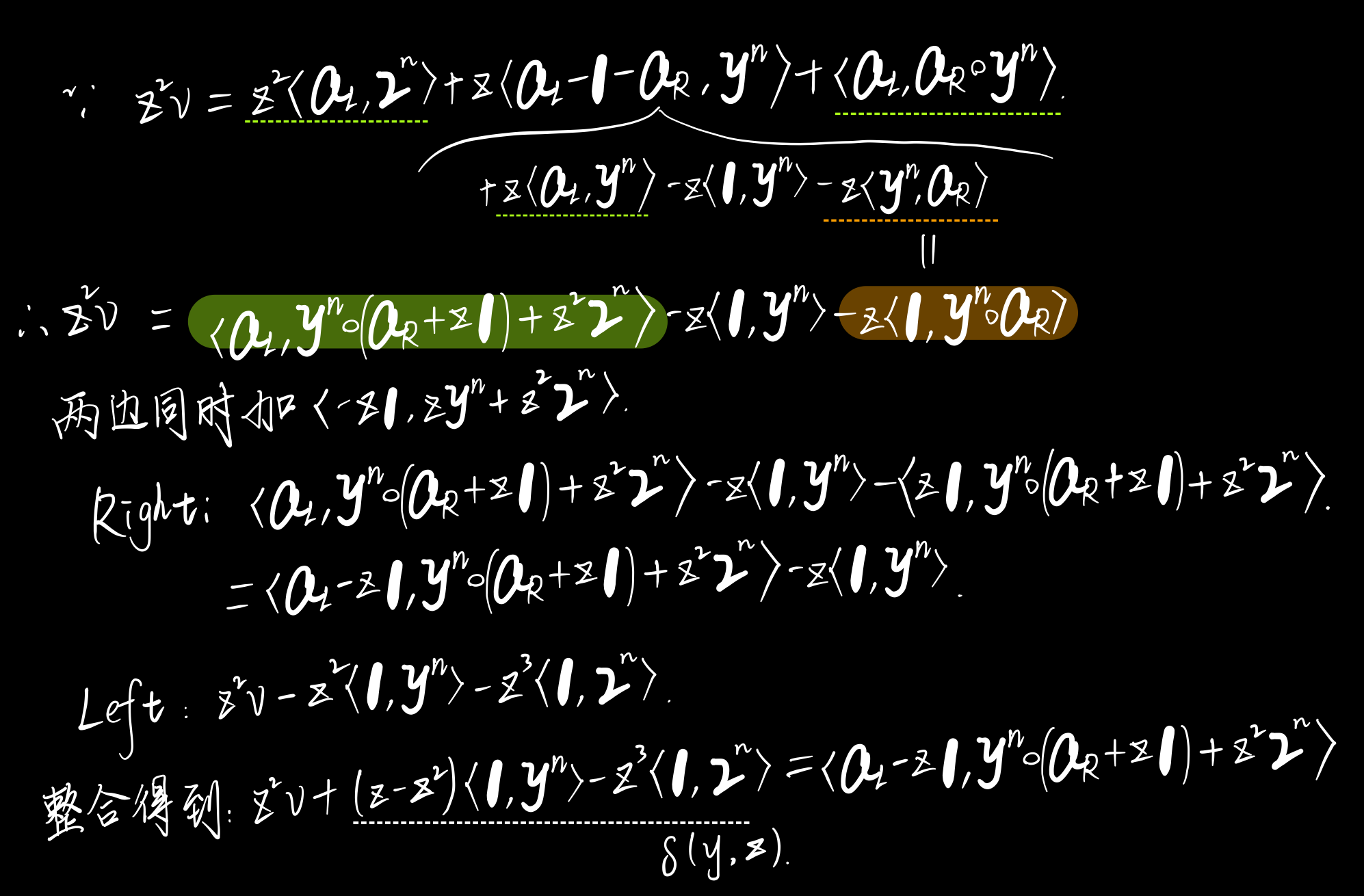
将此时内积的左侧记作unblinded l(X)，右侧记作unblinded r(X)

下面是盲化后新定义的多项式$l(X),r(X)$，以及二次多项式$t(X)$：

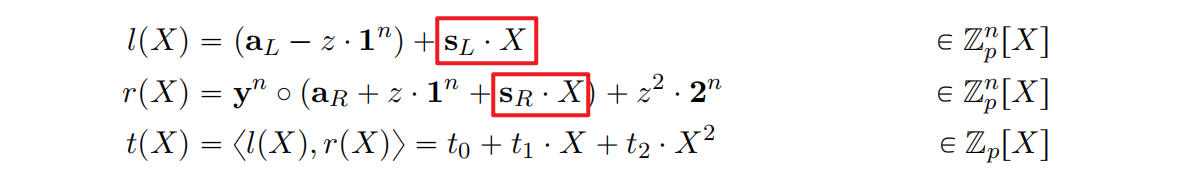
Prover需要证明$t_0=z^2v+\delta(y,z)$，$l(X),r(X)$正确，以及$t(X)=\langle l(X),r(X)\rangle$

---

$\mathcal{P}$ computes:

$\quad\tilde{t_1},\tilde{t_2}\longleftarrow\mathbb{Z}_p$

$\quad T_i=t_1B+\tilde{t_1}\tilde{B}\in\mathbb{G},\quad i=\{1,2\}$

$\mathcal{P}\rightarrow\mathcal{V}:T_1,T_2$

$\mathcal{V}:x\longleftarrow\mathbb{Z}^{*}_{p}\quad(\mathbb{Z}_{p}\backslash\{0\})$

$\mathcal{V}\rightarrow\mathcal{P}:x$ // a random challenge

$\mathcal{P}$ computes:

$\quad\textbf{l}=l(x)=\textbf{a}_L+\textbf{s}_L\cdot x-z\cdot\textbf{1}\in\mathbb{Z}^{n}_{p}$

$\quad\textbf{r}=r(x)=\textbf{y}^{n}\circ(\textbf{a}_R+\textbf{s}_R\cdot x+z\cdot\textbf{1})+z^2\cdot\textbf{2}^n\in\mathbb{Z}^{n}_{p}$

$\quad\textbf{t}=t(x)=\langle\textbf{l},\textbf{r}\rangle\in\mathbb{Z}_p$

$\quad\tilde{t}=z^2\cdot\tilde{v}+\tilde{t_1}\cdot x+\tilde{t_2}\cdot x^2\in\mathbb{Z}_p$ // blinding value for $\textbf{t}$

$\quad\tilde{e}=\tilde{a}+\tilde{s}\cdot x\in\mathbb{Z}_p$ // $\tilde{a},\tilde{s}$ blind $A,S$

$\mathcal{P}\rightarrow\mathcal{V}:\textbf{t},\tilde{t},\tilde{e},\textbf{l},\textbf{r}$

---

而更在上述（分割线内）步骤之前，还需要先于”$\mathcal{V}\rightarrow\mathcal{P}:challenge\ value\ y$”，$\mathcal{P}\rightarrow\mathcal{V}:commitment\ A,S$：

$A=\langle\textbf{a}_L,\textbf{G}\rangle+\langle\textbf{a}_R,\textbf{H}\rangle+\tilde{a}\tilde{B}$

$S=\langle\textbf{s}_L,\textbf{G}\rangle+\langle\textbf{s}_R,\textbf{H}\rangle+\tilde{s}\tilde{B}$

但需要对复合变量$\textbf{y}^{n}\circ\textbf{a}_R,\textbf{y}^{n}\circ\textbf{s}_R$作出承诺，且

$Com(\textbf{a}_L,\textbf{a}_R,\tilde{a})=\langle\textbf{a}_L,\textbf{G}\rangle+\langle\textbf{a}_R,\textbf{H}\rangle+\tilde{a}\tilde{B}=\langle\textbf{a}_L,\textbf{G}\rangle+\langle\textbf{y}^n\circ\textbf{a}_R,\textbf{y}^{-n}\circ\textbf{H}\rangle+\tilde{a}\tilde{B}$

因此令$\textbf{H’}=\textbf{y}^{-n}\circ\textbf{H}$，即$H_i^{‘}=y^{-i+1}\cdot H_i,\quad i=1,…,n$

由 Verifier 将原commitment A, S变形为对应$\textbf{H’}$以及复合变量的commitment

---

All based on ECDLP

$\textbf{t}B+\tilde{t}\tilde{B}\stackrel{?}{=}z^{2}V+\delta(y,z)B+T_1\cdot x+T_2\cdot x^2$ // ① check that $\textbf{t}=z^2v+\delta(y,z)+t_1x+t_2x^2$

$A+S\cdot x-z\langle\textbf{1},\textbf{G}\rangle+\langle z\textbf{y}^n+z^2\textbf{2}^n,\textbf{H’}\rangle-\tilde{e}\tilde{B}\stackrel{?}{=}\langle\textbf{l},\textbf{G}\rangle+\langle\textbf{r},\textbf{H’}\rangle$ // ② check that $l(X),r(X)$ are correct

$\textbf{t}\stackrel{?}{=}\langle\textbf{l},\textbf{r}\rangle$ // ③ check that $t(X)=\langle l(X),r(X)\rangle$

---

但校验②③：Prover和Verifier之间直接传输$\textbf{l},\textbf{r}$，导致需要$2n$个标量的带宽

Logarithmic Range Proof

内积协议一般用于证明以下关系：

$$\{(\textbf{G},\textbf{H}\in\mathbb{G}^n,P\in\mathbb{G},c\in\mathbb{Z}_p;\ \textbf{a},\textbf{b}\in\mathbb{Z}^{n}_{p}):\ P=\textbf{aG}+\textbf{bH}\wedge c=\langle\textbf{a},\textbf{b}\rangle\}$$

等价于证明：

$$\{(\textbf{G},\textbf{H}\in\mathbb{G}^n,u,P\in\mathbb{G};\ \textbf{a},\textbf{b}\in\mathbb{Z}^{n}_{p}):\ P=\textbf{aG}+\textbf{bH}+\langle\textbf{a},\textbf{b}\rangle u\}$$

引入中间变量$x\in\mathbb{Z}_{p}^{\times}$，记$n’=n/2$，对原始的$\textbf{a},\textbf{b},\textbf{G},\textbf{H}$作以下变换：

$$\textbf{a}'=x\textbf{a}_{[:n']}+x^{-1}\textbf{a}_{[n':]}\in\mathbb{Z}_p^{n'}\\ \textbf{b}'=x^{-1}\textbf{b}_{[:n']}+x\textbf{b}_{[n':]}\in\mathbb{Z}_p^{n'}\\ \textbf{G}'=x^{-1}\textbf{G}_{[:n']}+x\textbf{G}_{[n':]}\in\mathbb{G}^{n'}\\ \textbf{H}'=x\textbf{H}_{[:n']}+x^{-1}\textbf{H}_{[n':]}\in\mathbb{G}^{n'}\\$$

令$P’=\langle\textbf{a}’,\textbf{G}’\rangle+\langle\textbf{b}’,\textbf{H}’\rangle+\langle\textbf{a}’,\textbf{b}’\rangle u$

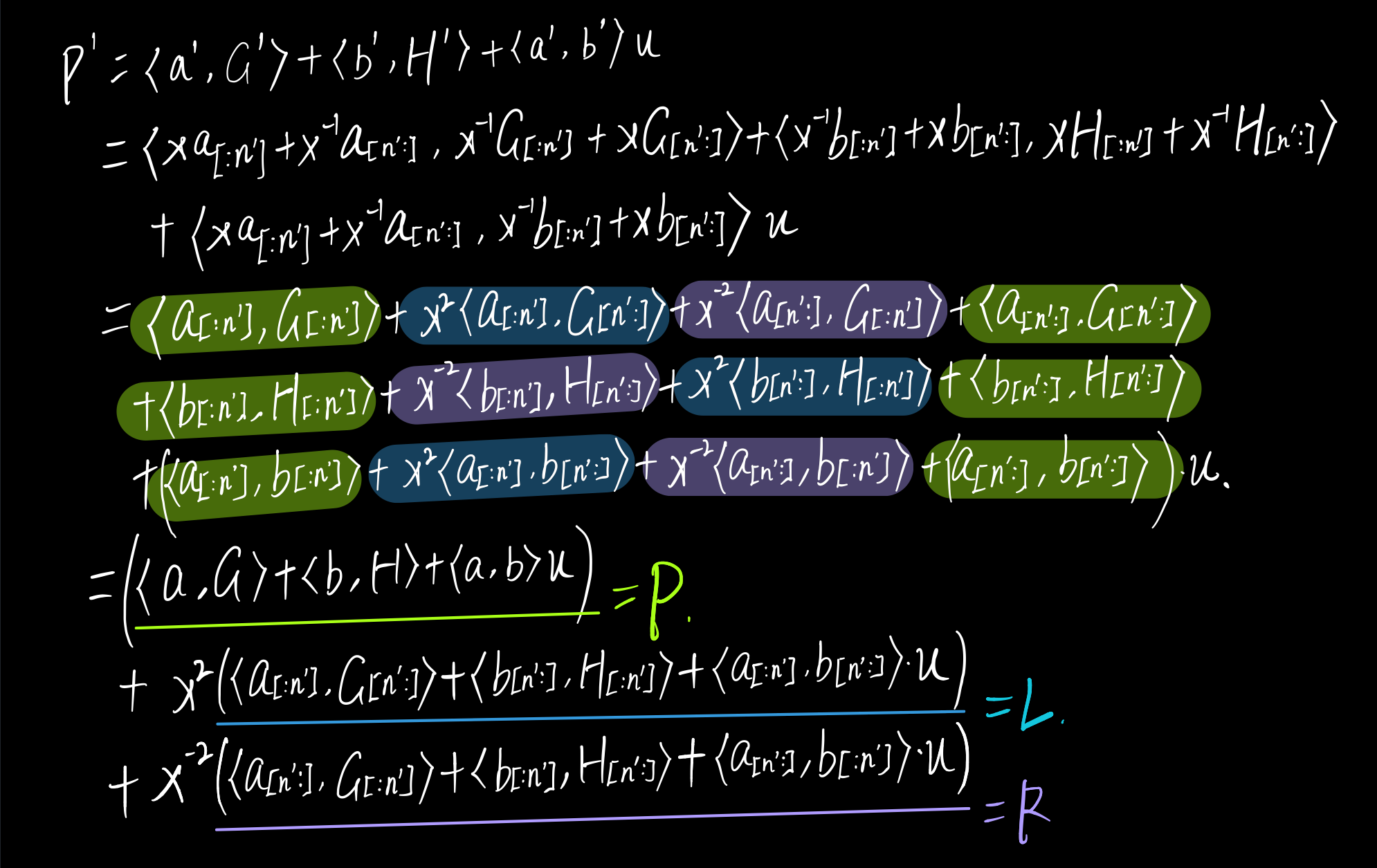
当$P=\textbf{aG}+\textbf{bH}+\langle\textbf{a},\textbf{b}\rangle u$成立时，上述推导成立，即$P’=P+x^2L+x^{-2}R$

此时传输的$\textbf{a},\textbf{b}$就转为了$\textbf{a}’,\textbf{b}’$（带宽/2）

因此我们可以递归压缩$P$（记作$P^{(0)}$），得到

$P^{(k)}=\langle\textbf{a}^{(k)},\textbf{G}^{(k)}\rangle+\langle\textbf{b}^{(k)},\textbf{H}^{(k)}\rangle+\langle\textbf{a}^{(k)},\textbf{b}^{(k)}\rangle u$

$P^{(k)}=P^{(0)}+\sum_{i=1}^{k}(x^2L^{(i-1)}+x^{-2}R^{(i-1)})$

此时Verifier只需验证

$$P^{(0)}\stackrel{?}{=}\langle\textbf{a}^{(k)},\textbf{G}^{(k)}\rangle+\langle\textbf{b}^{(k)},\textbf{H}^{(k)}\rangle+\langle\textbf{a}^{(k)},\textbf{b}^{(k)}\rangle u-\sum_{i=1}^{k}(x^2L^{(i-1)}+x^{-2}R^{(i-1)})$$

即可

Proofer需要发送$(\textbf{a}^{(k)},\textbf{b}^{(k)})$以及$k$轮的$(L,R)$，消耗带宽从$2n$降到了$2logn+2$.

将前文的校验②③改用这种方法，来实现对数级的压缩。

Aggregating Logarithmic Proofs

红框中为$\sum_{j=1}^{m}(z^{1+j})$，而非$\sum z^2$，是因为下面原有式子中的$z^{2}$，在$m$个individual range proofs整合时，采用不同的幂次$z^{3},z^{4},…$（仍然成立）

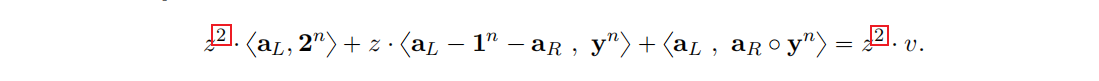
进一步的，定义新的 $\tilde{t}=\tilde{t_1}\cdot x+\tilde{t_2}\cdot x^2+\sum_{j=1}^{m}z^{1+j}\cdot\tilde{v_j}$ （其中$\tilde{v_j}$为对应$v_j$的盲化因子，$j=1,…,m$）

$\delta(y,z)=(z-z^2)\langle\textbf{1}^{n\cdot m},\textbf{y}^{n\cdot m}\rangle-\sum_{j=1}^{m}z^{j+2}\langle\textbf{1}^{n},\textbf{2}^{n}\rangle$

前文的校验①改写为：

$$\textbf{t}B+\tilde{t}\tilde{B}\stackrel{?}{=}z^{2}\langle\textbf{z}^{m},\textbf{V}\rangle+\delta(y,z)B+T_1\cdot x+T_2\cdot x^2\\ ,其中\ \textbf{V}=(V_1,V_2,...,V_m)\in\mathbb{G}^{m},\textbf{z}^{m}=(1,z,z^2,...,z^{m-1})\in\mathbb{Z}_{p}^{m}$$

校验②的左侧改写为：

$$A+S\cdot x-z\langle\textbf{1}^{n\cdot m},\textbf{G}\rangle+\langle z\textbf{y}^{n\cdot m}+\sum_{j=1}^{m}z^{1+j}\cdot(\textbf{0}^{(j-1)n}\|\textbf{2}^n\|\textbf{0}^{(m-j)n},\textbf{H'}\rangle-\tilde{e}\tilde{B}$$

Non-Interactive Proof through Fiat-Shamir

Fiat-Shamir直观表示可看知乎回答https://zhuanlan.zhihu.com/p/95921725

TODO